题目内容
若二次方程式x2+ax+93=0二根为r,s,且x2-22x+b=0二根为r+1,s+1,则b= .
考点:根与系数的关系
专题:计算题
分析:根据根与系数的关系得到rs=93,r+1+s+1=22,(r+1)(s+1)=b,则r+s=20,然后把(r+1)(s+1)展开后利用整体代入的方法计算即可.
解答:解:根据题意得rs=93,r+1+s+1=22,(r+1)(s+1)=b,
所以r+s=20,
而b=rs+r+s+1,
所以b=93+20+1=114.
故答案为114.
所以r+s=20,
而b=rs+r+s+1,
所以b=93+20+1=114.
故答案为114.
点评:本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
 如图,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B,C.若∠A=40°,则∠ABX+∠ACX=( )
如图,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B,C.若∠A=40°,则∠ABX+∠ACX=( )| A、25° | B、30° |
| C、45° | D、50° |
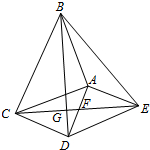 如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交CE于点G,连接BE.下列结论中:
如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交CE于点G,连接BE.下列结论中: ∠A=20°,AB=BC=CD=DE=EF,则∠CDE等于
∠A=20°,AB=BC=CD=DE=EF,则∠CDE等于