题目内容
4.阅读以下材料:高斯是德国著名的大科学家,他最出名的故事就是在他10岁时,小学老师出了一道算术难题:计算1+2+3+…+100=?
在其他同学还在犯难时,却很快传来了高斯的声音:“老师,我已经算好了!”
老师很吃惊,高斯解释道:因为1+100=101,2+99=101,3+98=101,…,49+52=101,50+51=101,而像这样的等于101的组合一共有50组,所以答案很快就可以求出:101×50=5050.
根据以上的信息,请同学们:
(1)计算1+3+5+7+…+99的值.
(2)计算2+4+6+8+…+200的值.
(3)用含a和n的式子表示运算结果:求a+2a+3a+…+na的值.
分析 利用连续的整数相加等于两端的数相加乘数的个数除以2,直接列式分别计算得出答案即可.
解答 解:(1)原式=(1+99)×50÷2
=100×25
=2500;
(2)原式=2×(1+2+3+…+100)
=2×5050
=10100;
(3)原式=a(1+2+…+n)
=$\frac{1}{2}$an(1+n).
点评 此题考查数字的变化规律,找出数字运算的特点,得出数字的运算规律,利用规律解决问题.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
12.下列四个命题中,假命题是( )
| A. | 两角对应相等,两个三角形相似 | |
| B. | 三边对应成比例,两个三角形相似 | |
| C. | 两边对应成比例且其中一边的对角相等,两个三角形相似 | |
| D. | 两边对应成比例且夹角相等,两个三角形相似 |
19.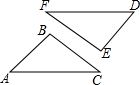 如图,△ABC≌△DEF,∠A=50°,∠B=100°,则∠F的度数是( )
如图,△ABC≌△DEF,∠A=50°,∠B=100°,则∠F的度数是( )
 如图,△ABC≌△DEF,∠A=50°,∠B=100°,则∠F的度数是( )
如图,△ABC≌△DEF,∠A=50°,∠B=100°,则∠F的度数是( )| A. | 30° | B. | 50° | C. | 60° | D. | 100° |
13.一件衬衫先按成本加价60元标价,再以8折出售,仍可获利24元,这件衬衫的成本是多少钱?设衬衫的成本为x元.
(1)填写下表:(用含有x的代数式表示)
(2)根据相等关系列出方程:(0.8x+48)-x=24.
(1)填写下表:(用含有x的代数式表示)
| 成本 | 标价 | 售价 |
| x | x+60 | 0.8x+48 |
 (a、b均为正数),字母的值都扩大为原来的2倍,则分式的值( )
(a、b均为正数),字母的值都扩大为原来的2倍,则分式的值( ) C. 不变 D. 缩小为原来的
C. 不变 D. 缩小为原来的
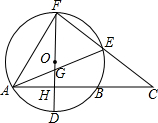 如图,⊙O的直径FD⊥弦AB于点H,E是$\widehat{BF}$上一动点,连结FE并延长交AB的延长线于点C,AB=8,HD=2.
如图,⊙O的直径FD⊥弦AB于点H,E是$\widehat{BF}$上一动点,连结FE并延长交AB的延长线于点C,AB=8,HD=2.