题目内容
16.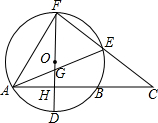 如图,⊙O的直径FD⊥弦AB于点H,E是$\widehat{BF}$上一动点,连结FE并延长交AB的延长线于点C,AB=8,HD=2.
如图,⊙O的直径FD⊥弦AB于点H,E是$\widehat{BF}$上一动点,连结FE并延长交AB的延长线于点C,AB=8,HD=2.(1)求⊙O的直径FD;
(2)在E点运动的过程中,EF•CF的值是否为定值?若是,求出其定值;若不是,请说明理由;
(3)当E点运动到$\widehat{DBF}$的中点时,连接AE交DF于点G,求△FEA的面积.
分析 (1)连接OA,由垂径定理得到AH=$\frac{1}{2}$AB=4,设OA=x,在Rt△OAH中,根据勾股定理列方程即可得到结论;
(2)根据垂径定理得到$\widehat{AF}=\widehat{BF}$,根据圆周角定理得到∠BAF=∠AEF,推出△FAE∽△FCA,根据相似三角形的性质得到$\frac{AF}{CF}=\frac{EF}{AF}$,推出AF2=EF•CF,代入数据即可得到结论;
(3)连接OE,由E点是$\widehat{DBF}$的中点,得到∠FAE=45°,∠EOF=90°,于是得到∠EOH=∠AHG,推出△OGE∽△HGA,根据相似三角形的性质得到$\frac{OE}{AH}=\frac{OG}{HG}$,求得OG=$\frac{5}{3}$,得到FG=OF+OG=$\frac{20}{3}$,根据三角形的面积公式即可得到结论.
解答 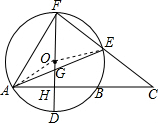 解:(1)连接OA,
解:(1)连接OA,
∵直径FD⊥弦AB于点H,
∴AH=$\frac{1}{2}$AB=4,
设OA=x,
在Rt△OAH中,AO2=AH2+(x-2)2,
即x2=42+(x-2)2,
∴x=5,
∴DF=2OA=10;
(2)是,
∵直径FD⊥弦AB于点H,
∴$\widehat{AF}=\widehat{BF}$,
∴∠BAF=∠AEF,
∵∠AFE=∠CFA,
∴△FAE∽△FCA,
∴$\frac{AF}{CF}=\frac{EF}{AF}$,
∴AF2=EF•CF,
在Rt△AFH中,
AF2=AH2+FH2=44+82=80,
∴EF•CF=80;
(3)连接OE,
∵E点是$\widehat{DBF}$的中点,
∴∠FAE=45°,∠EOF=90°,
∴∠EOH=∠AHG,
∵∠OGE=∠HGA,
∴△OGE∽△HGA,
∴$\frac{OE}{AH}=\frac{OG}{HG}$,
即$\frac{5}{4}$=$\frac{OG}{3-OG}$,
∴OG=$\frac{5}{3}$,
∴FG=OF+OG=$\frac{20}{3}$,
∴S△FEA=S△EFG+S△AFG=$\frac{1}{2}$FG•OE+$\frac{1}{2}$FG•AH=$\frac{1}{2}×\frac{20}{3}$×(4+5)=30.
点评 本题考查了垂径定理,勾股定理相似三角形的判定和性质,圆周角定理,正确的作出辅助线是解题的关键.

| A. | 两点确定一条直线 | B. | 射线AB也可以写作射线BA | ||
| C. | 等角的余角相等 | D. | 同角的补角相等 |
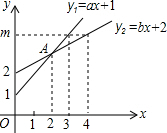 已知射线y1=ax+1与射线y2=bx+2在同一平面直角坐标系中的图象如图所示,则下列说法中①a=2b;②m=4;③点A的坐标为(2,3),正确的( )
已知射线y1=ax+1与射线y2=bx+2在同一平面直角坐标系中的图象如图所示,则下列说法中①a=2b;②m=4;③点A的坐标为(2,3),正确的( ) 桌面上放着1个长方体和1个圆柱体,按如图所示的方式摆放在一起,不是其三视图的是( )
桌面上放着1个长方体和1个圆柱体,按如图所示的方式摆放在一起,不是其三视图的是( )



 如图,直线AB、CD相交于点O,OE是∠AOC的角平分线,且∠DOE=5∠COE,求∠AOC的度数.
如图,直线AB、CD相交于点O,OE是∠AOC的角平分线,且∠DOE=5∠COE,求∠AOC的度数.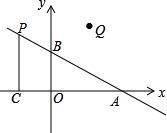 如图,在平面直角坐标系中,O是坐标原点,点A的坐标为(4,0),点B的坐标为(0,b)(b>0),点P是直线AB上位于第二象限内的一个动点,过点P作PC⊥x轴于点C,记点P关于y轴的对称点为Q,设点P的横坐标为a.
如图,在平面直角坐标系中,O是坐标原点,点A的坐标为(4,0),点B的坐标为(0,b)(b>0),点P是直线AB上位于第二象限内的一个动点,过点P作PC⊥x轴于点C,记点P关于y轴的对称点为Q,设点P的横坐标为a.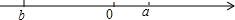 已知有理数a,b在数轴上的位置如图所示.
已知有理数a,b在数轴上的位置如图所示.