题目内容
13．已知两条抛物线P和Q的解析式分别是关于y与x的关系式：P：y=x2-2mx-m2与Q：y=x2-2mx-（m2+1）．对上述抛物线说法正确的序号是（ ）
①两条抛物线与y轴的交点一定不在x轴的上方；
②在抛物线P、Q中，可以将其中一条抛物线经过向上或向下平移得到另一条抛物线；
③在抛物线P、Q中，可以将其中一条抛物线经过向左或向右平移得到另一条抛物线；
④两条抛物线的顶点之间的距离为1．
| A． | ①② | B． | ①③④ | C． | ①②④ | D． | ①②③④ |
分析 ①求出抛物线与y轴的交点即可判断；
②根据两抛物线对称轴相同，可知其中一条抛物线经过向上或向下平移得到另一条抛物线；
③根据两抛物线对称轴相同，可知两条抛物线不可能左右平移得到；
④配方后得到顶点坐标，相减即可．
解答 解：①P与y轴交点为（0，-m2），Q与y轴交点为（0，-（m2+1）），一定不在x轴的上方，故本选项正确；
②由于两抛物线对称轴相同，均为x=m，可知，其中一条抛物线经过向上或向下平移得到另一条抛物线；故本选项正确；
③由于两抛物线对称轴相同，两条抛物线不可能左右平移得到，故本选项错误；
④P配方得，y=x2-2mx+m2-2m2=（x-m）2-2m2；Q配方得，y=x2-2mx+m2-m2-m2-1=（x-m）2-2m2-1，-2m2-（-2m2-1）=1，故本选项正确．
故选C．
点评 本题考查了二次函数的性质，熟悉二次函数与x轴、y轴的交点的求法，图象的平移、顶点坐标的求法是解题的关键．
练习册系列答案
相关题目
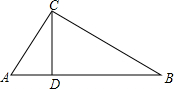如图，在△ABC中，∠ACB=90°，CD⊥AB，垂足为D，若∠B=32°，CD=6，求AB的长．（结果保留到0.1）（已知sin32°=0.5299，cos32°=0.8480，tan32°=0.6249）
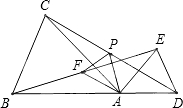如图，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE，点B、A、D在同一条直线上，连接BE、CD，F、P分别为BE、CD的中点，连接AF、AP、PF．
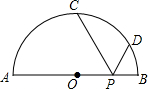如图，AB是半径为R的半圆的直径，C、D是半圆周上的两点，已知$\widehat{AC}$、$\widehat{BD}$的度数分别是90°和30°，动点P在线段AB上，则PC+PD的最小值是$\sqrt{3}$R．
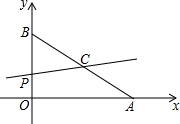如图，平面直角坐标系中，已知点A（4，0）和点B（0，3），点C是AB的中点，点P在折线AOB上，直线CP截△AOB，所得的三角形与△AOB相似，那么点
3．已知一水池的容积V（公升）与注入水的时间t（分钟）之间开始是一次函数关系，表中记录的是这段时间注入水的时间与水池容积部分对应值．
（1）求这段时间时V关于t的函数关系式（不需要写出函数的定义域）；
（2）从t为25分钟开始，每分钟注入的水量发生变化了，到t为27分钟时，水池的容积为726公升，如果这两分钟中的每分钟注入的水量增长的百分率相同，求这个百分率．
| 注入水的时间t（分钟） | 0 | 10 | … | 25 |
| 水池的容积V（公升） | 100 | 300 | … | 600 |
（2）从t为25分钟开始，每分钟注入的水量发生变化了，到t为27分钟时，水池的容积为726公升，如果这两分钟中的每分钟注入的水量增长的百分率相同，求这个百分率．