题目内容
1. 如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE,∠BOF=15°,求∠AOC的度数.
如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE,∠BOF=15°,求∠AOC的度数.
分析 设∠BOD为x,根据角平分线的定义用x表示出∠BOF,列方程求出x,根据对顶角相等得到答案.
解答 解:设∠BOD为x,
∵OE平分∠BOD,
∴∠DOE=∠BOE=$\frac{1}{2}$x,
∴∠COE=180°-$\frac{1}{2}$x,
∵OF平分∠COE,
∴∠EOF=90°-$\frac{1}{4}$x,
则∠BOF=90°-$\frac{1}{4}$x-$\frac{1}{2}$x=15°,
解得x=100°,
∴∠AOC=∠BOD=100°.
点评 本题考查的是对顶角的性质和角平分线的定义,掌握对顶角相等、从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线是解题的关键,注意方程思想的应用.

练习册系列答案
相关题目
12.现有四种说法:①-a表示负数;②若|x|=-x,则x<0;③绝对值最小的有理数是0;④若|a|=|b|,则a=b;⑤若a<b<0,则|a|>|b|,其中正确的是( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
11.原产量n千克减产20%之后的产量应为( )
| A. | (1+20%)n千克 | B. | (1-20%)n千克 | C. | (n-20%)千克 | D. | 20% n千克 |
 结合图形计算:$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+$\frac{1}{16}$+$\frac{1}{32}$+$\frac{1}{64}$+$\frac{1}{128}$=$\frac{127}{128}$.
结合图形计算:$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+$\frac{1}{16}$+$\frac{1}{32}$+$\frac{1}{64}$+$\frac{1}{128}$=$\frac{127}{128}$.
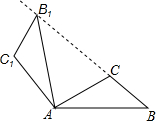 如图,将△ABC绕点A按逆时针方向旋转100°,得到△AB1C1,若点B1在线段BC的延长线上,则∠BB1C1的大小是80度.
如图,将△ABC绕点A按逆时针方向旋转100°,得到△AB1C1,若点B1在线段BC的延长线上,则∠BB1C1的大小是80度.