题目内容
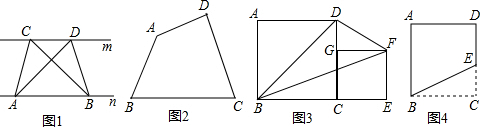
如果图1,已知直线m∥n,A、B为直线n上两定点,C、D为直线m上两动点,容易证明:△ABC的面积=△ABD的面积;
问题探究
(1)在图2中画出与四边形ABCD面积相等且以AB为一条边的三角形.
(2)在图3中,已知正方形ABCD的边长为4,G是边CD上一点,以CD为边作正方形GCEF,当CG=a时,求△BDF的面积.
问题解决
(3)李大爷家有一块正方形的果园如图4所示,由于修建道路,图中三角形BCE区域将被占用,现决定在DE右侧补给一块土地,补偿后,果园将调整为四边形ABMD,要求补偿后的四边形ABMD的面积与原来形正方形ABCD的面积相等且M在射线BE上.请你在图4中通过画图来确定M点的位置,并简要叙述画法和理由;若AB=4,CE=a,求出上图中tan∠MDC的值.

问题探究
(1)在图2中画出与四边形ABCD面积相等且以AB为一条边的三角形.
(2)在图3中,已知正方形ABCD的边长为4,G是边CD上一点,以CD为边作正方形GCEF,当CG=a时,求△BDF的面积.
问题解决
(3)李大爷家有一块正方形的果园如图4所示,由于修建道路,图中三角形BCE区域将被占用,现决定在DE右侧补给一块土地,补偿后,果园将调整为四边形ABMD,要求补偿后的四边形ABMD的面积与原来形正方形ABCD的面积相等且M在射线BE上.请你在图4中通过画图来确定M点的位置,并简要叙述画法和理由;若AB=4,CE=a,求出上图中tan∠MDC的值.
考点:四边形综合题
专题:
分析:(1)(2)利用平行线根据题目信息得出三角形的面积相等;
(3)同理,通过作平行线利用三角形面积相等进行转化,得出图形面积与原来面积相等.
(3)同理,通过作平行线利用三角形面积相等进行转化,得出图形面积与原来面积相等.
解答:解:(1)如图2所示:

连接AC,过点D作AC的平行线交BC的延长线于点E,连接AE,△ABE即为所求的三角形;
(2)连接CF,如图3所示:

∵BD、CF分别为正方形ABCD和正方形GCEF的对角线,
∴∠BDC=∠DCF=45°,
∴BD∥CF,
∴S△BDF=S△CBD;
(3)连接BD,过点C作BD的平行线交BE的延长线于M,连接DM,如图4所示:

则S△BDM=S△CBD,
∴S△BDM-S△BDE=S△CBD-S△BDE,
即:S△DME=S△ECB,
∴补偿后的四边形的面积与原来的正方形ABCD的面积相等且M在射线BP上.

连接AC,过点D作AC的平行线交BC的延长线于点E,连接AE,△ABE即为所求的三角形;
(2)连接CF,如图3所示:

∵BD、CF分别为正方形ABCD和正方形GCEF的对角线,
∴∠BDC=∠DCF=45°,
∴BD∥CF,
∴S△BDF=S△CBD;
(3)连接BD,过点C作BD的平行线交BE的延长线于M,连接DM,如图4所示:

则S△BDM=S△CBD,
∴S△BDM-S△BDE=S△CBD-S△BDE,
即:S△DME=S△ECB,
∴补偿后的四边形的面积与原来的正方形ABCD的面积相等且M在射线BP上.
点评:本题考查了信息获取能力,读懂题目信息,构造出平行线是利用三角形面积相等进行转化求解三角形面积的关键.

练习册系列答案
相关题目
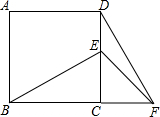 在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C顺时针旋转90°,得到△DFC,连接EF,若∠BEC=60°,则∠EFD等于( )
在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C顺时针旋转90°,得到△DFC,连接EF,若∠BEC=60°,则∠EFD等于( )| A、10° | B、25° |
| C、20° | D、15° |
下列说法中,错误的是( )
| A、直线AB和直线BA是同一条直线 |
| B、三条直线两两相交必有三个交点 |
| C、线段MN是直线MN的一部分 |
| D、三条直线两两相交,可能只有一个交点 |
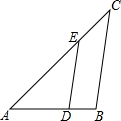 如图所示,已知DE∥BC,AE=50cm,EC=30cm,BC=70cm,∠A=45°,∠C=40°,求:
如图所示,已知DE∥BC,AE=50cm,EC=30cm,BC=70cm,∠A=45°,∠C=40°,求: 如图,已知线段AC,点D为AC的中点,BC=
如图,已知线段AC,点D为AC的中点,BC=
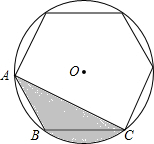 如图,在半径为6cm的圆内画一个正六边形,求阴影部分的面积.
如图,在半径为6cm的圆内画一个正六边形,求阴影部分的面积. 已知y是关于x的函数,函数图象如图所示,则当y>0时,自变量x的取值范围是
已知y是关于x的函数,函数图象如图所示,则当y>0时,自变量x的取值范围是