题目内容
有两根木条,一根AB长为50,另一根CD长为90,在它们的中点处各有一个小圆孔M、N(圆孔直径忽略不计,M、N抽象成两点),将它们的一端重合,放置在同一条直线上,画出草图,并求此时两根木条的小圆孔之间MN的长度.


考点:一元一次方程的应用,两点间的距离
专题:几何图形问题
分析:本题在画图时,应考虑到A、B、M、N四点之间的位置关系的多种可能,再根据题意正确地画出图形解题.
解答:解:本题有两种情形:
(1)当A、C(或B、D)重合,且剩余两端点在重合点同侧时,

MN=CN-AM=
CD-
AB=45-25=20(厘米);
(2)当B、C(或A、C)重合,且剩余两端点在重合点两侧时,

MN=CN+BM=
CD+
AB=45+25=70(厘米).
故两根木条的小圆孔之间MN的长度是20cm或70cm.
(1)当A、C(或B、D)重合,且剩余两端点在重合点同侧时,

MN=CN-AM=
| 1 |
| 2 |
| 1 |
| 2 |
(2)当B、C(或A、C)重合,且剩余两端点在重合点两侧时,

MN=CN+BM=
| 1 |
| 2 |
| 1 |
| 2 |
故两根木条的小圆孔之间MN的长度是20cm或70cm.
点评:考查了一元一次方程的应用,两点间的距离,正确画图很重要,本题渗透了分类讨论的思想,体现了思维的严密性,在今后解决类似的问题时,要防止漏解.

练习册系列答案
相关题目
下列计算正确的是( )
| A、(2x+3y)2=4x2+9y2 | ||||||||||
B、(-c+
| ||||||||||
C、(
| ||||||||||
| D、(2a+5b)2=4a2+10ab+25b2 |
下列各选项中的两个图形不一定相似的是( )
| A、两个正方形 |
| B、两个等边三角形 |
| C、各有100°角的两个等腰三角形 |
| D、各有45°角的两个等腰三角形 |
等边三角形的一条边长为2,它的面积是( )
| A、4 | ||
B、
| ||
| C、3 | ||
D、2
|
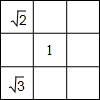 如图,试在图中填上恰当的数,使得图中每一行,每一列,每条对角线上3个数的乘积都等于1,你还能找到一个数,使得图中每一行,每一列,每一条对角线上3个数的乘积都等于这个数吗?
如图,试在图中填上恰当的数,使得图中每一行,每一列,每条对角线上3个数的乘积都等于1,你还能找到一个数,使得图中每一行,每一列,每一条对角线上3个数的乘积都等于这个数吗? 有理数a、b、c在数轴上的对应点如图,化简代数式:|a-b|+|a+b|-|c-a|+2|b-c|.
有理数a、b、c在数轴上的对应点如图,化简代数式:|a-b|+|a+b|-|c-a|+2|b-c|.
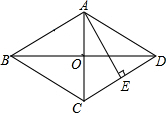 在菱形ABCD中,对角线AC与BD相交于点O,AE⊥CD于点E,且AE=OD,求∠ADC的度数.
在菱形ABCD中,对角线AC与BD相交于点O,AE⊥CD于点E,且AE=OD,求∠ADC的度数.