题目内容
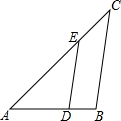 如图所示,已知DE∥BC,AE=50cm,EC=30cm,BC=70cm,∠A=45°,∠C=40°,求:
如图所示,已知DE∥BC,AE=50cm,EC=30cm,BC=70cm,∠A=45°,∠C=40°,求:(1)∠AED和∠ADE的大小;
(2)DE的长.
考点:相似三角形的判定与性质
专题:
分析:(1)如图,运用平行线的性质、三角形的内角和定理,证明∠AED=∠C=40°,∠ADE=∠B=95°.
(2)如图,运用相似三角形的判定定理证明△ADE∽△ABC,列出比例式
=
,求出DE即可解决问题.
(2)如图,运用相似三角形的判定定理证明△ADE∽△ABC,列出比例式
| AE |
| AC |
| DE |
| BC |
解答: 解:(1)如图,∵DE∥BC,∠C=40°,
解:(1)如图,∵DE∥BC,∠C=40°,
∴∠AED=∠C=40°,∠ADE=∠B;
∵∠A=45°,∠C=40°,
∵∠B=180°-45°-40°=95°,
∴∠ADE=95°,
即∠AED和∠ADE的大小分别为40°、95°.
(2)∵DE∥BC,
∴△ADE∽△ABC,
∴
=
,而AE=50,EC=30,BC=70,
∴DE=
(cm).
 解:(1)如图,∵DE∥BC,∠C=40°,
解:(1)如图,∵DE∥BC,∠C=40°,∴∠AED=∠C=40°,∠ADE=∠B;
∵∠A=45°,∠C=40°,
∵∠B=180°-45°-40°=95°,
∴∠ADE=95°,
即∠AED和∠ADE的大小分别为40°、95°.
(2)∵DE∥BC,
∴△ADE∽△ABC,
∴
| AE |
| AC |
| DE |
| BC |
∴DE=
| 350 |
| 8 |
点评:该题主要考查了三角形的内角和定理、平行线的性质、相似三角形的判定及其性质等几何知识点及其应用问题;数形结合,准确找出图形中隐含的相似三角形是解题的关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
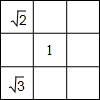 如图,试在图中填上恰当的数,使得图中每一行,每一列,每条对角线上3个数的乘积都等于1,你还能找到一个数,使得图中每一行,每一列,每一条对角线上3个数的乘积都等于这个数吗?
如图,试在图中填上恰当的数,使得图中每一行,每一列,每条对角线上3个数的乘积都等于1,你还能找到一个数,使得图中每一行,每一列,每一条对角线上3个数的乘积都等于这个数吗? 如图,△BCD的各个顶点都在⊙A上,△BCD的角平分线BF交CD于点E,交⊙A于点F,连结CF,求证:BE2=BC•BD-EC•ED.
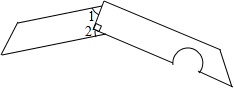
如图,△BCD的各个顶点都在⊙A上,△BCD的角平分线BF交CD于点E,交⊙A于点F,连结CF,求证:BE2=BC•BD-EC•ED. 有理数a、b、c在数轴上的对应点如图,化简代数式:|a-b|+|a+b|-|c-a|+2|b-c|.
有理数a、b、c在数轴上的对应点如图,化简代数式:|a-b|+|a+b|-|c-a|+2|b-c|.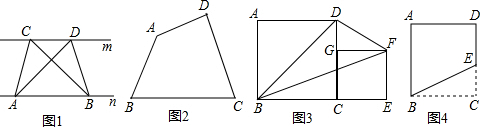
 利用网格作图(要求所画的三角形的顶点必须在格点上)
利用网格作图(要求所画的三角形的顶点必须在格点上)