题目内容
4. 已知:如图,⊙O中的弦AB与弦CD交于点P,点M、N分别是AB、CD的中点,$\widehat{AC}$=$\widehat{BD}$,求证:△PMN是等腰三角形.
已知:如图,⊙O中的弦AB与弦CD交于点P,点M、N分别是AB、CD的中点,$\widehat{AC}$=$\widehat{BD}$,求证:△PMN是等腰三角形.
分析 连结OM,ON,OA,OD,根据等弧对等弦得AB=CD,根据垂径定理得AM=DN,在Rt△OMA和Rt△OND中,根据勾股定理得到OM=ON,根据等腰三角形的性质和角的和差关系得到∠PMN=∠PNM,根据等腰三角形的判定即可求解.
解答 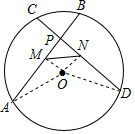 证明:连结OM,ON,OA,OD,
证明:连结OM,ON,OA,OD,
∵$\widehat{AC}$=$\widehat{BD}$,
∴$\widehat{AB}$=$\widehat{CD}$,
∴AB=CD,
∵点M、N分别是AB、CD的中点,
∴∠OMA=∠OMP=90°,∠OND=∠ONP=90°,AM=$\frac{1}{2}$AB,DN=$\frac{1}{2}$CD,
∴AM=DN,
∵OA=OD,
在Rt△OMA和Rt△OND中,OM=$\sqrt{O{A}^{2}-A{M}^{2}}$,ON=$\sqrt{O{D}^{2}-D{N}^{2}}$,
∴OM=ON,
∴∠OMN=∠ONM,
∴∠PMN=∠PNM,
∴PM=PN,
∴△PMN是等腰三角形.
点评 此题考查了圆心角、弧、弦的关系,等腰三角形的判定,垂径定理,勾股定理,等腰三角形的性质,关键是证明OM=ON.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
14.某小学为了了解各年级留守儿童的数量,对一到六年级留守儿童数量进行了统计,得到每个年级的留守儿童人数分别为10,15,10,17,18,20.对于这组数据,下列说法错误的是( )
| A. | 平均数是15 | B. | 众数是10 | C. | 中位数是17 | D. | 方差是$\frac{44}{3}$ |
 如图,直线l同侧有A、B两点,请利用直尺和圆规在直线l上求作一点P,使AP+BP值最小.(不写作法,保留作图痕迹)
如图,直线l同侧有A、B两点,请利用直尺和圆规在直线l上求作一点P,使AP+BP值最小.(不写作法,保留作图痕迹)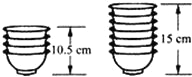 如图,两摞规格相同的碗整齐地叠放在桌面上,请根据图中给出的数据信息,解答下列问题:
如图,两摞规格相同的碗整齐地叠放在桌面上,请根据图中给出的数据信息,解答下列问题: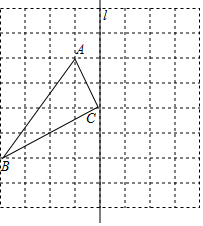 如图,在8×8的正方形网格中,每个小正方形的边长都是1,已知△ABC的三个顶点在格点上.
如图,在8×8的正方形网格中,每个小正方形的边长都是1,已知△ABC的三个顶点在格点上.