题目内容
10.[x]表示不超过x的最大整数,则满足条件$\left\{\begin{array}{l}{[x]+[2x]=[{x}^{2}]}\\{x<\frac{5}{2}}\end{array}\right.$的x的取值范围是0≤x<0.5或$\sqrt{6}$≤x<$\frac{5}{2}$.分析 由[x]+[2x]=[x2],可知x≥0,由于x<$\frac{5}{2}$,再分情况:0≤x<0.5,0.5≤x<1,1≤x<1.5,1.5≤x<2,2≤x<$\frac{5}{2}$,进行讨论即可得到x的取值范围.
解答 解:∵[x]+[2x]=[x2],
∴x≥0,
∵x<$\frac{5}{2}$,
∴0≤x<0.5,[x]+[2x]=0+0=0,[x2]=0,符合题意,
0.5≤x<1,[x]+[2x]=0+1=1,[x2]=0,不符合题意,
1≤x<1.5,[x]+[2x]=1+2=3,[x2]=1或2,不符合题意,
1.5≤x<2,[x]+[2x]=1+3=4,[x2]=2或3,不符合题意,
2≤x<$\sqrt{6}$,[x]+[2x]=2+4=6,[x2]=4或5,不符合题意,
$\sqrt{6}$≤x<$\frac{5}{2}$,[x]+[2x]=2+4=6,[x2]=6,符合题意.
综上所述,x的取值范围是0≤x<0.5或$\sqrt{6}$≤x<$\frac{5}{2}$.
故答案为:0≤x<0.5或$\sqrt{6}$≤x<$\frac{5}{2}$.
点评 考查了取整计算,首先根据[x]+[2x]=[x2],可知x≥0,注意分类思想的应用,关键是找到区间,有一定的难度.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
19.以下生活现象中,属于旋转变换得是( )
| A. | 钟表的指针和钟摆的运动 | B. | 站在电梯上的人的运动 | ||
| C. | 坐在火车上睡觉 | D. | 地下水位线逐年下降 |

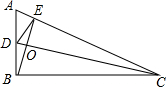 如图,D、E分别是△ABC的边AB、AC上的点,BE、CD相交于点O,且AD•AB=AE•AC,△OEC与△ODB相似吗?为什么?
如图,D、E分别是△ABC的边AB、AC上的点,BE、CD相交于点O,且AD•AB=AE•AC,△OEC与△ODB相似吗?为什么?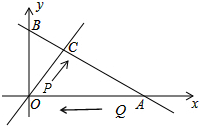 如图,直线m:y=kx(k>0)与直线n:y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$相交于点C,点A、B为直线n与坐标轴的交点,∠COA=60°,点P从O点出发沿线段OC向点C匀速运动,速度为每秒1个单位,同时点Q从点A出发沿线段AO向点O匀速运动,速度为每秒2个单位,设运动时间为t秒.
如图,直线m:y=kx(k>0)与直线n:y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$相交于点C,点A、B为直线n与坐标轴的交点,∠COA=60°,点P从O点出发沿线段OC向点C匀速运动,速度为每秒1个单位,同时点Q从点A出发沿线段AO向点O匀速运动,速度为每秒2个单位,设运动时间为t秒.