题目内容
1.已知反比例函数y=$\frac{6}{x}$,当x>3时,y的取值范围是0<y<2.分析 根据反比例函数的性质可以得到反比例函数y=$\frac{6}{x}$,当x>3时,y的取值范围.
解答 解:∵y=$\frac{6}{x}$,6>0,
∴当x>0时,y随x的增大而减小,当x=3时,y=2,
∴当x>3时,y的取值范围是0<y<2,
故答案为:0<y<2.
点评 本题考查反比例函数的性质,解答本题的关键是明确题意,利用反比例函数的性质解答.

练习册系列答案
相关题目
12.下面调查中,适合采用普查的是( )
| A. | 调查你所在的班级同学的身高情况 | B. | 调查全国中学生心理健康现状 | ||
| C. | 调查我市食品合格情况 | D. | 调查中央电视台《少儿节目》收视率 |
13.关于x的一元一次不等式$\frac{m-2x}{3}$≤-2的解集为x≥4,则m的值为( )
| A. | 14 | B. | 7 | C. | -2 | D. | 2 |
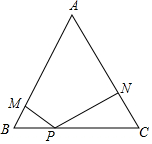 在边长为2的等边三角形ABC中,P是BC边上任意一点,过点 P分别作 PM⊥A B,PN⊥AC,M、N分别为垂足.
在边长为2的等边三角形ABC中,P是BC边上任意一点,过点 P分别作 PM⊥A B,PN⊥AC,M、N分别为垂足.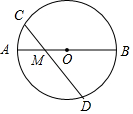 如图,AB是⊙O的直径,AB=4,点M是OA的中点,过点M的直线与⊙O交于C、D两点.若∠CMA=45°,则弦CD的长为$\sqrt{14}$.
如图,AB是⊙O的直径,AB=4,点M是OA的中点,过点M的直线与⊙O交于C、D两点.若∠CMA=45°,则弦CD的长为$\sqrt{14}$. 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,-4),B(3,-3),C(1,-1).
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,-4),B(3,-3),C(1,-1).