题目内容
11．已知$\frac{a}{b}$=$\frac{c}{d}$=$\frac{e}{f}$=$\frac{2}{3}$，则a+c+e=6，则b+d+f=（ ）| A． | 12 | B． | 9 | C． | 6 | D． | 4 |
分析 由$\frac{a}{b}$=$\frac{c}{d}$=$\frac{e}{f}$=$\frac{2}{3}$得a=$\frac{2}{3}$b、c=$\frac{2}{3}$d、e=$\frac{2}{3}$f，代入到a+c+e=6可得答案．
解答 解：由$\frac{a}{b}$=$\frac{c}{d}$=$\frac{e}{f}$=$\frac{2}{3}$得a=$\frac{2}{3}$b、c=$\frac{2}{3}$d、e=$\frac{2}{3}$f，
则$\frac{2}{3}$b+$\frac{2}{3}$d+$\frac{2}{3}$f=6，
即$\frac{2}{3}$（b+d+f）=6，
∴b+d+f=6×$\frac{3}{2}$=9，
故选：B．
点评 本题主要考查比例的基本性质，熟练掌握比例的基本性质和等式的性质是解题的关键．
练习册系列答案
科学实验活动册系列答案
相关题目
5．用公式法解x2+3x=1时，先求出a、b、c的值，则a、b、c依次为（ ）
| A． | 1，3，1 | B． | 1，3，-1 | C． | -1，-3，-1 | D． | -1，3，1 |
6．
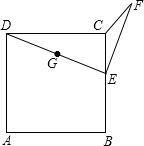如图，已知正方形ABCD的边长为10，E在BC边上运动，取DE的中点G，EG绕点E顺时针旋转90°得EF，问CE长为多少时，A、C、F三点在一条直线上（ ）
如图，已知正方形ABCD的边长为10，E在BC边上运动，取DE的中点G，EG绕点E顺时针旋转90°得EF，问CE长为多少时，A、C、F三点在一条直线上（ ）| A． | $\frac{8}{3}$ | B． | $\frac{6}{5}$ | C． | $\frac{10}{3}$ | D． | $\frac{3}{2}$ |
3．一个多边形的每个外角都等于30°，则这个多边形的边数是（ ）
| A． | 10 | B． | 11 | C． | 12 | D． | 13 |
6．代数式（22+1）（24+1）（28+1）…（232+1）+1的个位数是（ ）
| A． | 4 | B． | 0 | C． | 6 | D． | 2 |
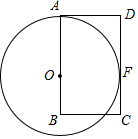如图，矩形ABCD中，AB=9，O是AB边上一点，以O为圆心，OA为半径画圆与边CD相切于点F，与BC相交于点E，若EC=2，则⊙O的半径为5．
已知：直线L和L外一点P，根据所学的“用尺规作一个角等于已知角”