题目内容
6.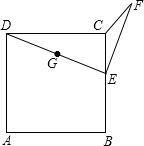 如图,已知正方形ABCD的边长为10,E在BC边上运动,取DE的中点G,EG绕点E顺时针旋转90°得EF,问CE长为多少时,A、C、F三点在一条直线上( )
如图,已知正方形ABCD的边长为10,E在BC边上运动,取DE的中点G,EG绕点E顺时针旋转90°得EF,问CE长为多少时,A、C、F三点在一条直线上( )| A. | $\frac{8}{3}$ | B. | $\frac{6}{5}$ | C. | $\frac{10}{3}$ | D. | $\frac{3}{2}$ |
分析 过F作BC的垂线,交BC延长线于N点,连接AF.只要证明Rt△FNE∽Rt△ECD,利用相似比2:1解决问题.再证明△CNF是等腰直角三角形即可解决问题.
解答 解:过F作BC的垂线,交BC延长线于N点,连接AF.
∵∠DCE=∠ENF=90°,∠DEC+∠NEF=90°,∠NEF+∠EFN=90°,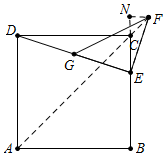
∴∠DEC=∠EFN,
∴Rt△FNE∽Rt△ECD,
∵DE的中点G,EG绕E顺时针旋转90°得EF,
∴两三角形相似比为1:2,
∴可以得到CE=2NF,NE=$\frac{1}{2}$CD=5.
∵AC平分正方形直角,
∴∠NFC=45°,
∴△CNF是等腰直角三角形,
∴CN=NF,
∴CE=$\frac{2}{3}$NE=$\frac{2}{3}$×5=$\frac{10}{3}$,
故选C.
点评 此题考查了相似三角形的判定与性质、正方形的性质以及直角三角形的性质.此题难度适中,解题的关键是构造Rt△FNE∽Rt△ECD,求得△FCN是等腰直角三角形,然后根据相似三角形的性质求解.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
16.已知点P(0,m)在y轴的正半轴上,则点M(-m,-m-1)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
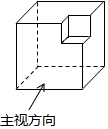 将一个边长为3cm的大立方体挖去一个边长为1cm的小立方体,得到的几何体如图所示,则下列选项中.不是如图所示几何体的主视图、左视图、俯视图之一的是( )
将一个边长为3cm的大立方体挖去一个边长为1cm的小立方体,得到的几何体如图所示,则下列选项中.不是如图所示几何体的主视图、左视图、俯视图之一的是( )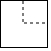
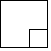
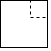
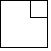
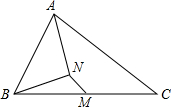 如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,且AB=10,BC=15,MN=3,则AC的长是( )
如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,且AB=10,BC=15,MN=3,则AC的长是( ) 如图,在等边△ABC中,AB=4,P、M、N分别是BC、CA、AB边上动点,则PM+MN的最小值是2$\sqrt{3}$.
如图,在等边△ABC中,AB=4,P、M、N分别是BC、CA、AB边上动点,则PM+MN的最小值是2$\sqrt{3}$.