题目内容
6.代数式(22+1)(24+1)(28+1)…(232+1)+1的个位数是( )| A. | 4 | B. | 0 | C. | 6 | D. | 2 |
分析 原式变形为$\frac{1}{3}$(22-1)(22+1)(24+1)(28+1)…(232+1)+1,反复利用平方差公式计算即可得到结果.
解答 解:(22+1)(24+1)(28+1)…(232+1)+1
=$\frac{1}{3}$×(22-1)(22+1)(24+1)(28+1)…(232+1)+1
=$\frac{1}{3}$×(24-1)(24+1)(28+1)…(232+1)+1
=$\frac{1}{3}$(264-1)+1
=$\frac{{2}^{64}+2}{3}$,
∵21=2,22=4,23=8,24=16,25=32,…,
∴个位上数字以2,4,8,6为循环节循环,
∵64÷4=16,
∴264个位上数字为6,即原式个位上数字为6.
故选C
点评 此题考查了平方差公式,熟练掌握平方差公式是解本题的关键.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
15.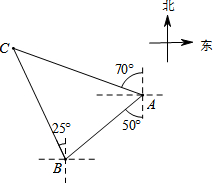 如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是( )
如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是( )
 如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是( )
如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是( )| A. | 10$\sqrt{2}$海里 | B. | 10$\sqrt{3}$海里 | C. | 10$\sqrt{6}$海里 | D. | 20$\sqrt{6}$海里 |
16. 如图是某个几何体的三视图,该几何体是( )
如图是某个几何体的三视图,该几何体是( )
 如图是某个几何体的三视图,该几何体是( )
如图是某个几何体的三视图,该几何体是( )| A. | 圆锥 | B. | 三棱锥 | C. | 四棱锥 | D. | 四棱柱 |
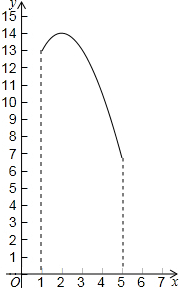
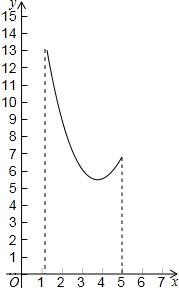
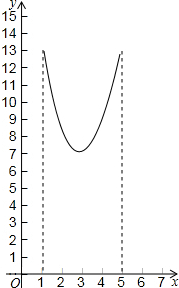
 如图,在等边△ABC中,AB=4,P、M、N分别是BC、CA、AB边上动点,则PM+MN的最小值是2$\sqrt{3}$.
如图,在等边△ABC中,AB=4,P、M、N分别是BC、CA、AB边上动点,则PM+MN的最小值是2$\sqrt{3}$.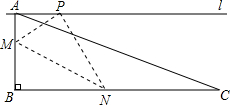 如图,在三角形纸片ABC中,∠ABC=90°,AB=5,BC=13,过点A,作直线l∥BC,折叠三角形纸片ABC,使点B落在直线l上的P处,折痕为MN.当点P在直线l上移动时,折痕的端点M、N也随之移动.若限定端点M、N分别在AB、BC边上移动,若设AP的长为x,MN的长为y,则下列选项,能表示y与x之间的函数关系的大致图象是( )
如图,在三角形纸片ABC中,∠ABC=90°,AB=5,BC=13,过点A,作直线l∥BC,折叠三角形纸片ABC,使点B落在直线l上的P处,折痕为MN.当点P在直线l上移动时,折痕的端点M、N也随之移动.若限定端点M、N分别在AB、BC边上移动,若设AP的长为x,MN的长为y,则下列选项,能表示y与x之间的函数关系的大致图象是( )