题目内容
12.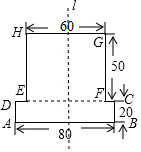 如图是由两个长方形组成的工件平面图(单位:mm),直线l是它的对称轴,若HG=60,AB=80,GF=50,CB=20,则能完全覆盖这个平面图形的圆面的最小半径是50mm.
如图是由两个长方形组成的工件平面图(单位:mm),直线l是它的对称轴,若HG=60,AB=80,GF=50,CB=20,则能完全覆盖这个平面图形的圆面的最小半径是50mm.
分析 根据已知条件得到CM=30,AN=40,根据勾股定理列方程得到OM=40,由勾股定理得到结论.
解答 解:如图,设圆心为O,
连接AO,CO,
∵直线l是它的对称轴,
∴CM=30,AN=40,
∵CM2+OM2=AN2+ON2,
∴302+OM2=402+(70-OM)2,
解得:OM=40,
∴OC=$\sqrt{3{0}^{2}+4{0}^{2}}$=50,
∴能完全覆盖这个平面图形的圆面的最小半径是50mm.
故答案为:50.
点评 本题考查的圆内接四边形,是垂径定理,根据题意画出图形,利用数形结合进行解答是解答此题的关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
3.某商品的价格标签已丢失,售货员只知道它的进价为80元,打七折售出后,仍可获利5%,你认为标签上的价格为( )元.
| A. | 110 | B. | 120 | C. | 130 | D. | 140 |
20.下列图形,对称轴最多的是( )
| A. | 正方形 | B. | 等边三角形 | C. | 角 | D. | 线段 |
7. 如图,在△ABC中,D为AB中点,DE∥BC交AC于E点,则△ADE与△ABC的面积比为( )
如图,在△ABC中,D为AB中点,DE∥BC交AC于E点,则△ADE与△ABC的面积比为( )
 如图,在△ABC中,D为AB中点,DE∥BC交AC于E点,则△ADE与△ABC的面积比为( )
如图,在△ABC中,D为AB中点,DE∥BC交AC于E点,则△ADE与△ABC的面积比为( )| A. | 1:1 | B. | 1:2 | C. | 1:3 | D. | 1:4 |
2.用配方法解一元二次方程x2-6x-1=0时,方程可变形为( )
| A. | (x-3)2=10 | B. | (x-6)2=37 | C. | (x-3)2=4 | D. | (x-3)2=1 |
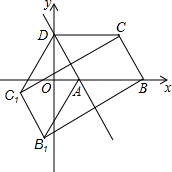 如图,已知?ABCD的三个顶点A(n,0),B(m,0),D(0,2n)(m>n>0),作?ABCD关于直线AD的对称图形AB1C1D.
如图,已知?ABCD的三个顶点A(n,0),B(m,0),D(0,2n)(m>n>0),作?ABCD关于直线AD的对称图形AB1C1D.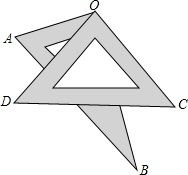 如图所示,将一副三角板重叠放在一起,使两直角顶点重合于点O
如图所示,将一副三角板重叠放在一起,使两直角顶点重合于点O