题目内容
1．已知一个口袋中装有5个只有颜色不同的球，其中有3个白球，2个黑球．（1）求从中随机取出一个球是黑球的概率是多少；
（2）若往口袋中再放入x个白球和8个黑球，从口袋中随机取出一个白球的概率是$\frac{1}{3}$，求x的值．
分析 （1）由从中随机取出一个球共有5种情况，其中是黑球的有2种可能，根据概率公式计算可得；
（2）利用概率公式：白球数量÷球的总数=取得白球的概率，列出关于x的分式方程，解之可得．
解答 解：（1）∵从中随机取出一个球共有5种情况，其中是黑球的有2种可能，
∴从中随机取出一个球是黑球的概率是$\frac{2}{5}$；
（2）根据题意可得：$\frac{3+x}{5+x+8}$=$\frac{1}{3}$，
解得：x=2，
经检验x=2是分式方程的解，
∴x=2．
点评 本题主要考查概率公式和分式方程的应用，掌握随机事件A的概率P（A）=事件A可能出现的结果数÷所有可能出现的结果数是解题的关键．
练习册系列答案
相关题目
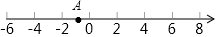如图，已知点A在数轴上，从点A出发，沿数轴向右移动3个单位长度到达点C，点B所表示的有理数是5的相反数，按要求完成下列各小题．
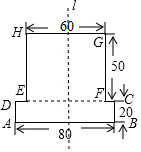如图是由两个长方形组成的工件平面图（单位：mm），直线l是它的对称轴，若HG=60，AB=80，GF=50，CB=20，则能完全覆盖这个平面图形的圆面的最小半径是50mm．
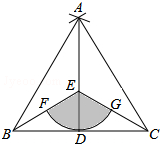如图，点D是线段BC的中点，分别以点B，C为圆心，BC长为半径画弧，两弧相交于点A，连接AB，AC，AD，点E是AD上一点（不与点A，D重合），连接BE，CE，以点E为圆心，ED长为半径画弧，分别交BE，CE于点F，G，若BC=6，∠EBC=45°，则图中阴影部分的面积为$\frac{9}{2}$π．