题目内容
20.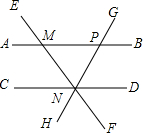 如图,AB∥CD,直线EF与AB,CD分别交于点M,N,过点N的直线GH与AB交于点P,则下列结论错误的是( )
如图,AB∥CD,直线EF与AB,CD分别交于点M,N,过点N的直线GH与AB交于点P,则下列结论错误的是( )| A. | ∠EMB=∠END | B. | ∠BMN=∠MNC | C. | ∠CNH=∠BPG | D. | ∠DNG=∠AME |
分析 根据平行线的性质,找出各相等的角,再去对照四个选项即可得出结论.
解答 解:A、∵AB∥CD,
∴∠EMB=∠END(两直线平行,同位角相等);
B、∵AB∥CD,
∴∠BMN=∠MNC(两直线平行,内错角相等);
C、∵AB∥CD,
∴∠CNH=∠MPN(两直线平行,同位角相等),
∵∠MPN=∠BPG(对顶角),
∴∠CNH=∠BPG(等量代换);
D、∠DNG与∠AME没有关系,
无法判定其相等.
故选D.
点评 本题考查了平行线的性质,解题的关键是结合平行线的性质来对照四个选择.本题属于基础题,难度不大,解决该题型题目时,根据平行线的性质找出相等(或互补)的角是关键.

练习册系列答案
相关题目
10.小明用计算器计算(a+b)c的值,其按键顺序和计算器显示结果如表:

这时他才明白计算器是先做乘法再做加法的,于是他依次按键:

从而得到了正确结果,已知a是b的3倍,则正确的结果是( )

这时他才明白计算器是先做乘法再做加法的,于是他依次按键:

从而得到了正确结果,已知a是b的3倍,则正确的结果是( )
| A. | 24 | B. | 39 | C. | 48 | D. | 96 |
11.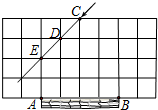 足球射门,不考虑其他因素,仅考虑射点到球门AB的张角大小时,张角越大,射门越好.如图的正方形网格中,点A,B,C,D,E均在格点上,球员带球沿CD方向进攻,最好的射点在( )
足球射门,不考虑其他因素,仅考虑射点到球门AB的张角大小时,张角越大,射门越好.如图的正方形网格中,点A,B,C,D,E均在格点上,球员带球沿CD方向进攻,最好的射点在( )
 足球射门,不考虑其他因素,仅考虑射点到球门AB的张角大小时,张角越大,射门越好.如图的正方形网格中,点A,B,C,D,E均在格点上,球员带球沿CD方向进攻,最好的射点在( )
足球射门,不考虑其他因素,仅考虑射点到球门AB的张角大小时,张角越大,射门越好.如图的正方形网格中,点A,B,C,D,E均在格点上,球员带球沿CD方向进攻,最好的射点在( )| A. | 点C | B. | 点D或点E | ||
| C. | 线段DE(异于端点) 上一点 | D. | 线段CD(异于端点) 上一点 |
8. 如图,在△ABC中,∠ACB=90°,CD∥AB,∠ACD=40°,则∠B的度数为( )
如图,在△ABC中,∠ACB=90°,CD∥AB,∠ACD=40°,则∠B的度数为( )
 如图,在△ABC中,∠ACB=90°,CD∥AB,∠ACD=40°,则∠B的度数为( )
如图,在△ABC中,∠ACB=90°,CD∥AB,∠ACD=40°,则∠B的度数为( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
9.下列说法正确的是( )
| A. | 为了审核书稿中的错别字,选择抽样调查 | |
| B. | 为了了解春节联欢晚会的收视率,选择全面调查 | |
| C. | “射击运动员射击一次,命中靶心”是随机事件 | |
| D. | “经过有交通信号灯的路口,遇到红灯”是必然事件 |
 如图,已知抛物线y=-x2+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0)
如图,已知抛物线y=-x2+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0) 如图是由4个大小相同的正方体组合而成的几何体,其主视图是( )
如图是由4个大小相同的正方体组合而成的几何体,其主视图是( )



 如图,矩形ABCD中,M、E、F三点在$\overline{AD}$上,N是矩形两对角线的交点.若$\overline{AB}$=24,$\overline{AD}$=32,$\overline{MD}$=16,$\overline{ED}$=8,$\overline{FD}$=7,则下列哪一条直线是A、C两点的对称轴?( )
如图,矩形ABCD中,M、E、F三点在$\overline{AD}$上,N是矩形两对角线的交点.若$\overline{AB}$=24,$\overline{AD}$=32,$\overline{MD}$=16,$\overline{ED}$=8,$\overline{FD}$=7,则下列哪一条直线是A、C两点的对称轴?( )