题目内容
12.观察下列式子:1×3+1=22;
7×9+1=82;
25×27+1=262;
79×81+1=802;
…
可猜想第2016个式子为(32016-2)×32016+1=(32016-1)2.
分析 观察等式两边的数的特点,用n表示其规律,代入n=2016即可求解.
解答 解:观察发现,第n个等式可以表示为:(3n-2)×3n+1=(3n-1)2,
当n=2016时,
(32016-2)×32016+1=(32016-1)2,
故答案为:(32016-2)×32016+1=(32016-1)2.
点评 此题主要考查数的规律探索,观察发现等式中的每一个数与序数n之间的关系是解题的关键.

练习册系列答案
相关题目
2. 如图,直线a,b被直线c所截,∠1与∠2的位置关系是( )
如图,直线a,b被直线c所截,∠1与∠2的位置关系是( )
 如图,直线a,b被直线c所截,∠1与∠2的位置关系是( )
如图,直线a,b被直线c所截,∠1与∠2的位置关系是( )| A. | 同位角 | B. | 内错角 | C. | 同旁内角 | D. | 对顶角 |
3.宁波栎社国际机场三期扩建工程建设总投资84.5亿元,其中84.5亿元用科学记数法表示为( )
| A. | 0.845×1010元 | B. | 84.5×108元 | C. | 8.45×109元 | D. | 8.45×1010元 |
20.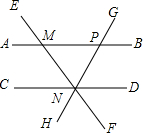 如图,AB∥CD,直线EF与AB,CD分别交于点M,N,过点N的直线GH与AB交于点P,则下列结论错误的是( )
如图,AB∥CD,直线EF与AB,CD分别交于点M,N,过点N的直线GH与AB交于点P,则下列结论错误的是( )
 如图,AB∥CD,直线EF与AB,CD分别交于点M,N,过点N的直线GH与AB交于点P,则下列结论错误的是( )
如图,AB∥CD,直线EF与AB,CD分别交于点M,N,过点N的直线GH与AB交于点P,则下列结论错误的是( )| A. | ∠EMB=∠END | B. | ∠BMN=∠MNC | C. | ∠CNH=∠BPG | D. | ∠DNG=∠AME |
7.在平面直角坐标系中,把一条抛物线先向上平移3个单位长度,然后绕原点旋转180°得到抛物线y=x2+5x+6,则原抛物线的解析式是( )
| A. | y=-(x-$\frac{5}{2}$)2-$\frac{11}{4}$ | B. | y=-(x+$\frac{5}{2}$)2-$\frac{11}{4}$ | C. | y=-(x-$\frac{5}{2}$)2-$\frac{1}{4}$ | D. | y=-(x+$\frac{5}{2}$)2+$\frac{1}{4}$ |
17.计算32×3-1的结果是( )
| A. | 3 | B. | -3 | C. | 2 | D. | -2 |

 2016年2月1日,我国在西昌卫星发射中心,用长征三号丙运载火箭成功将第5颗新一代北斗星送入预定轨道,如图,火箭从地面L处发射,当火箭达到A点时,从位于地面R处雷达站测得AR的距离是6km,仰角为42.4°;1秒后火箭到达B点,此时测得仰角为45.5°
2016年2月1日,我国在西昌卫星发射中心,用长征三号丙运载火箭成功将第5颗新一代北斗星送入预定轨道,如图,火箭从地面L处发射,当火箭达到A点时,从位于地面R处雷达站测得AR的距离是6km,仰角为42.4°;1秒后火箭到达B点,此时测得仰角为45.5°