题目内容
10. 如图,矩形ABCD中,M、E、F三点在$\overline{AD}$上,N是矩形两对角线的交点.若$\overline{AB}$=24,$\overline{AD}$=32,$\overline{MD}$=16,$\overline{ED}$=8,$\overline{FD}$=7,则下列哪一条直线是A、C两点的对称轴?( )
如图,矩形ABCD中,M、E、F三点在$\overline{AD}$上,N是矩形两对角线的交点.若$\overline{AB}$=24,$\overline{AD}$=32,$\overline{MD}$=16,$\overline{ED}$=8,$\overline{FD}$=7,则下列哪一条直线是A、C两点的对称轴?( )| A. | 直线MN | B. | 直线EN | C. | 直线FN | D. | 直线DN |
分析 根据题意可知A、C两点的对称轴是线段AC的垂直平分线,画出合适的辅助线,然后根据题意可以求得AC和AN的长,然后根据三角形相似的知识可以求得AP的长,从而可以得到P与哪一个点重合,本题得以解决.
解答 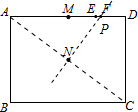 解:∵A、C两点的对称轴是线段AC的垂直平分线,
解:∵A、C两点的对称轴是线段AC的垂直平分线,
∴连接AC,过点N作AC的垂直平分线PN交AD于点P,
∵AB=24,AD=32,
∴$AC=\sqrt{2{4}^{2}+3{2}^{2}}=40$,
∴AN=20,
∵∠PAN=∠CAD,∠ANP=∠ADC,
∴△ANP∽△ADC,
∴$\frac{AN}{AD}=\frac{AP}{AC}$,
即$\frac{20}{32}=\frac{AP}{40}$,
解得,AP=25,
∵M、E、F三点在AD上,AD=32,MD=16,ED=8,FD=7,
∴AF=AD-FD=32-7=25,
∴点P与点F重合.
故选C.
点评 本题考查轴对称的性质、矩形的性质,解题的关键是明确题意,作出合适的辅助线,找出所求问题需要的条件.

练习册系列答案
相关题目
20.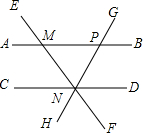 如图,AB∥CD,直线EF与AB,CD分别交于点M,N,过点N的直线GH与AB交于点P,则下列结论错误的是( )
如图,AB∥CD,直线EF与AB,CD分别交于点M,N,过点N的直线GH与AB交于点P,则下列结论错误的是( )
 如图,AB∥CD,直线EF与AB,CD分别交于点M,N,过点N的直线GH与AB交于点P,则下列结论错误的是( )
如图,AB∥CD,直线EF与AB,CD分别交于点M,N,过点N的直线GH与AB交于点P,则下列结论错误的是( )| A. | ∠EMB=∠END | B. | ∠BMN=∠MNC | C. | ∠CNH=∠BPG | D. | ∠DNG=∠AME |
15.下列调查中,最适合采用全面调查(普查)的是( )
| A. | 对重庆市居民日平均用水量的调查 | |
| B. | 对一批LED节能灯使用寿命的调查 | |
| C. | 对重庆新闻频道“天天630”栏目收视率的调查 | |
| D. | 对某校九年级(1)班同学的身高情况的调查 |
19.若$\sqrt{a-1}$+b2-4b+4=0,则ab的值等于( )
| A. | -2 | B. | 0 | C. | 1 | D. | 2 |
 2016年2月1日,我国在西昌卫星发射中心,用长征三号丙运载火箭成功将第5颗新一代北斗星送入预定轨道,如图,火箭从地面L处发射,当火箭达到A点时,从位于地面R处雷达站测得AR的距离是6km,仰角为42.4°;1秒后火箭到达B点,此时测得仰角为45.5°
2016年2月1日,我国在西昌卫星发射中心,用长征三号丙运载火箭成功将第5颗新一代北斗星送入预定轨道,如图,火箭从地面L处发射,当火箭达到A点时,从位于地面R处雷达站测得AR的距离是6km,仰角为42.4°;1秒后火箭到达B点,此时测得仰角为45.5° 如图,圆O通过五边形OABCD的四个顶点.若$\widehat{ABD}$=150°,∠A=65°,∠D=60°,则$\widehat{BC}$的度数为何?( )
如图,圆O通过五边形OABCD的四个顶点.若$\widehat{ABD}$=150°,∠A=65°,∠D=60°,则$\widehat{BC}$的度数为何?( )