题目内容
 如图所示,∠AOB=α,∠AOB内有一定点P,在∠AOB的两边上有两个动点Q、R(均不同与点O),△PQR周长最小时,记∠QPR的度数为β,则α与β满足的关系?
如图所示,∠AOB=α,∠AOB内有一定点P,在∠AOB的两边上有两个动点Q、R(均不同与点O),△PQR周长最小时,记∠QPR的度数为β,则α与β满足的关系?考点:轴对称-最短路线问题
专题:
分析:根据轴对称图形的性质,作出P关于OA、OB的对称点M、N,连接AB,根据两点之间线段最短得到最小值线段;然后根据对称的性质来求α与β满足的关系.
解答: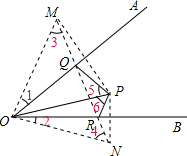 解:如图,分别作P关于OA、OB的对称点M、N.连接MN交OA、OB交于Q、R,则△PQR符合条件.
解:如图,分别作P关于OA、OB的对称点M、N.连接MN交OA、OB交于Q、R,则△PQR符合条件.
连接OM、ON.
根据对称的性质得到∠1+∠2=∠AOB=α,∠3+∠4=∠5+∠6=β.
∵∠1+∠2+∠AOB+∠3+∠4=180°,
∴2α+β=180°.
即α与β满足的关系是2α+β=180°.
 解:如图,分别作P关于OA、OB的对称点M、N.连接MN交OA、OB交于Q、R,则△PQR符合条件.
解:如图,分别作P关于OA、OB的对称点M、N.连接MN交OA、OB交于Q、R,则△PQR符合条件.连接OM、ON.
根据对称的性质得到∠1+∠2=∠AOB=α,∠3+∠4=∠5+∠6=β.
∵∠1+∠2+∠AOB+∠3+∠4=180°,
∴2α+β=180°.
即α与β满足的关系是2α+β=180°.
点评:此题考查了轴对称最短路径问题,根据题意构造出对称点,转化为三角形内角和的问题是解题的关键.

练习册系列答案
相关题目
已知某三角形的一条边长为a,一条边长为b,则这个三角形面积不可能为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知点A(x1,y1)、B(x2,y2)在双曲线y=-
上,且x1<x2,则y1,y2的大小关系是( )
| 2 |
| x |
| A、y1<y2 |
| B、y1>y2 |
| C、y1=y2 |
| D、都不对 |
 如图,AB∥CD,∠A、∠P、∠C三个角之间存在怎样的关系?
如图,AB∥CD,∠A、∠P、∠C三个角之间存在怎样的关系?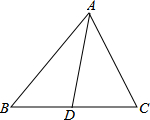 如图,△ABC中,D为BC中点.
如图,△ABC中,D为BC中点.