题目内容
2014年的世界杯足球赛在巴西举行.为了满足球迷的需要,某体育服装店老板计划到服装批发市场选购A、B两种品牌的服装.据市场调查得知,A款每套进价350元,B款每套进价200元,该店计划用不低于7600元且不高于8000元的资金订购30套A、B两款运动服.
(1)该店订购这两款运动服,共有哪几种方案?
(2)若该店以甲款每套400元,乙款每套300元的价格全部出售,哪种方案获利最大?
(1)该店订购这两款运动服,共有哪几种方案?
(2)若该店以甲款每套400元,乙款每套300元的价格全部出售,哪种方案获利最大?
考点:一元一次不等式组的应用
专题:
分析:(1)找到关键描述语“用不低于7600元且不高于8000元的资金订购30套甲、乙两款运动服”,进而找到所求的量的不等关系,列出不等式组求解.
(2)根据利润=售价-成本,分别求出甲款,乙款的利润相加后再比较,即可得出获利最大方案.
(2)根据利润=售价-成本,分别求出甲款,乙款的利润相加后再比较,即可得出获利最大方案.
解答:解:设该店订购甲款运动服x套,则订购乙款运动服(30-x)套,由题意,得
(1)
解这个不等式组,得
≤x≤
∵x为整数,∴x取11,12,13
∴30-x取19,18,17
答:方案①甲款11套,乙款19套;②甲款12套,乙款18套;③甲款13套,乙款17套;
(2)解法一:设该店全部出售甲、乙两款运动服后获利y元,
则y=(400-350)x+(300-200)(30-x)
=50x+3000-100x=-50x+3000.
∵-50<0,
∴y随x增大而减小,
∴当x=11时,y最大.
解法二:三种方案分别获利为:
方案一:(400-350)×11+(300-200)×19=2450(元)
方案二:(400-350)×12+(300-200)×18=2400(元)
方案三:(400-350)×13+(300-200)×17=2350(元)
∵2450>2400>2350.
∴方案一即甲款11套,乙款19套,获利最大.
答:甲款11套,乙款19套,获利最大.
(1)
|
解这个不等式组,得
| 32 |
| 3 |
| 40 |
| 3 |
∵x为整数,∴x取11,12,13
∴30-x取19,18,17
答:方案①甲款11套,乙款19套;②甲款12套,乙款18套;③甲款13套,乙款17套;
(2)解法一:设该店全部出售甲、乙两款运动服后获利y元,
则y=(400-350)x+(300-200)(30-x)
=50x+3000-100x=-50x+3000.
∵-50<0,
∴y随x增大而减小,
∴当x=11时,y最大.
解法二:三种方案分别获利为:
方案一:(400-350)×11+(300-200)×19=2450(元)
方案二:(400-350)×12+(300-200)×18=2400(元)
方案三:(400-350)×13+(300-200)×17=2350(元)
∵2450>2400>2350.
∴方案一即甲款11套,乙款19套,获利最大.
答:甲款11套,乙款19套,获利最大.
点评:本题考查一元一次不等式组的应用,将现实生活中的事件与数学思想联系起来,读懂题列出不等式关系式即可求解.

练习册系列答案
相关题目
 如图所示,∠AOB=α,∠AOB内有一定点P,在∠AOB的两边上有两个动点Q、R(均不同与点O),△PQR周长最小时,记∠QPR的度数为β,则α与β满足的关系?
如图所示,∠AOB=α,∠AOB内有一定点P,在∠AOB的两边上有两个动点Q、R(均不同与点O),△PQR周长最小时,记∠QPR的度数为β,则α与β满足的关系?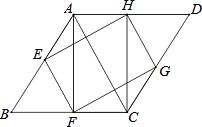 已知,如图,四边形ABCD是菱形,∠B是锐角,AF⊥BC于点F,CH⊥AD于点H,在AB边上取点E,使得AE=AH,在CD边上取点G,使得CG=CF,连接EF、FG、GH、HE.
已知,如图,四边形ABCD是菱形,∠B是锐角,AF⊥BC于点F,CH⊥AD于点H,在AB边上取点E,使得AE=AH,在CD边上取点G,使得CG=CF,连接EF、FG、GH、HE. 四边形ABCD是正方形,E在正方形外,CE∥BD,EB=BD,BE交DC于F,求证:∠BEC=30°.
四边形ABCD是正方形,E在正方形外,CE∥BD,EB=BD,BE交DC于F,求证:∠BEC=30°.