题目内容
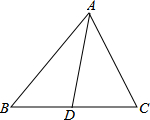 如图,△ABC中,D为BC中点.
如图,△ABC中,D为BC中点.(1)求证:AB+AC>2AD;
(2)若AB=5,AC=5,求AD的取值范围.
考点:全等三角形的判定与性质,三角形三边关系
专题:计算题
分析:(1)延长AD到E,使DE=AD,连接BE,再由D为BC中点得到BD=CD,夹角为对顶角相等,利用SAS得到三角形ADC与三角形EDB全等,利用全等三角形对应边相等得到AE=ED,在三角形ABE中,利用三角形三边关系即可得证;
(2)根据AB与AC的长,利用由三角形的三边关系,求出AD的范围即可.
(2)根据AB与AC的长,利用由三角形的三边关系,求出AD的范围即可.
解答: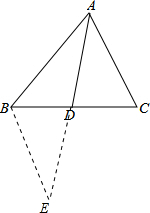 解:(1)延长AD到E,使DE=AD,连接BE,
解:(1)延长AD到E,使DE=AD,连接BE,
∵D为BC中点,
∴BD=CD,
在△ADC和△EDB中,
,
∴△ADC≌△EDB(SAS),
∴AD=ED,
在△ABE中,AB+EB>AE=2AD;
(2)∵5-5<2AD<5+5,
∴0<AD<5.
 解:(1)延长AD到E,使DE=AD,连接BE,
解:(1)延长AD到E,使DE=AD,连接BE,∵D为BC中点,
∴BD=CD,
在△ADC和△EDB中,
|
∴△ADC≌△EDB(SAS),
∴AD=ED,
在△ABE中,AB+EB>AE=2AD;
(2)∵5-5<2AD<5+5,
∴0<AD<5.
点评:此题考查了全等三角形的判定与性质,以及三角形的三边关系,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
下列各组数中互为相反数的是( )
A、-2与
| |||
B、-2与
| |||
C、-2与-
| |||
| D、2与|-2| |
 已知如图,AD∥BC,∠1=∠3,求证:∠B=∠D.
已知如图,AD∥BC,∠1=∠3,求证:∠B=∠D. 如图所示,∠AOB=α,∠AOB内有一定点P,在∠AOB的两边上有两个动点Q、R(均不同与点O),△PQR周长最小时,记∠QPR的度数为β,则α与β满足的关系?
如图所示,∠AOB=α,∠AOB内有一定点P,在∠AOB的两边上有两个动点Q、R(均不同与点O),△PQR周长最小时,记∠QPR的度数为β,则α与β满足的关系? 如图,AD∥BC,AD=BC,AE=CF.求证:
如图,AD∥BC,AD=BC,AE=CF.求证: 四边形ABCD是正方形,E在正方形外,CE∥BD,EB=BD,BE交DC于F,求证:∠BEC=30°.
四边形ABCD是正方形,E在正方形外,CE∥BD,EB=BD,BE交DC于F,求证:∠BEC=30°.