题目内容
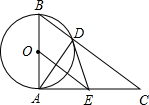 如图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.
如图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.(1)求证:ED是⊙O的切线.
(2)当OA=3,AE=4时,求BC的长度.
考点:切线的判定,垂径定理
专题:几何综合题
分析:(1)如图,连接OD.通过证明△AOE≌△DOE得到∠OAE=∠ODE=90°,易证得结论;
(2)利用圆周角定理和垂径定理推知OE∥BC,所以根据平行线分线段成比例求得BC的长度即可.
(2)利用圆周角定理和垂径定理推知OE∥BC,所以根据平行线分线段成比例求得BC的长度即可.
解答: (1)证明:如图,连接OD.
(1)证明:如图,连接OD.
∵AC⊥AB,
∴∠BAC=90°,即∠OAE=90°.
在△AOE与△DOE中,
,
∴△AOE≌△DOE(SSS),
∴∠OAE=∠ODE=90°,即OD⊥ED.
又∵OD是⊙O的半径,
∴ED是⊙O的切线;
(2)解:如图,在△OAE中,∠OAE=90°,OA=3,AE=4,
∴由勾股定理易求OE=5.
∵AB是直径,
∴∠ADB=90°,即AD⊥BC.
又∵由(1)知,△AOE≌△DOE,
∴∠AEO=∠DEO,
又∵AE=DE,
∴OE⊥AD,
∴OE∥BC,
∴
=
=
.
BC=2OE=10,即BC的长度是10.
 (1)证明:如图,连接OD.
(1)证明:如图,连接OD.∵AC⊥AB,
∴∠BAC=90°,即∠OAE=90°.
在△AOE与△DOE中,
|
∴△AOE≌△DOE(SSS),
∴∠OAE=∠ODE=90°,即OD⊥ED.
又∵OD是⊙O的半径,
∴ED是⊙O的切线;
(2)解:如图,在△OAE中,∠OAE=90°,OA=3,AE=4,
∴由勾股定理易求OE=5.
∵AB是直径,
∴∠ADB=90°,即AD⊥BC.
又∵由(1)知,△AOE≌△DOE,
∴∠AEO=∠DEO,
又∵AE=DE,
∴OE⊥AD,
∴OE∥BC,
∴
| OA |
| AB |
| OE |
| BC |
| 1 |
| 2 |
BC=2OE=10,即BC的长度是10.
点评:本题考查了切线的判定与性质.解答(2)题时,也可以根据三角形中位线定理来求线段BC的长度.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
细棒插入黄沙堆中,检验细棒是否垂直于地面常用的方法是( )
| A、合页型折纸检验法 |
| B、三角尺检验法 |
| C、铅垂线检验法 |
| D、长方形纸片检验法 |
 一般地,如果在一次实验中,结果落在区域D中每一个点都是等可能的,用A表示“实验结果落在D中的某个小区域M中”这个事件,那么事件A发生的概率PA=
一般地,如果在一次实验中,结果落在区域D中每一个点都是等可能的,用A表示“实验结果落在D中的某个小区域M中”这个事件,那么事件A发生的概率PA= 如图,AF平分∠BAO,DE平分∠CDO,AF∥DE.AB与CD有怎样的位置关系?为什么?
如图,AF平分∠BAO,DE平分∠CDO,AF∥DE.AB与CD有怎样的位置关系?为什么? 一水果贩子在批发市场按每千克1.8元批发了若干千克的西瓜进城出售,为了方便,他带了一些零钱备用.他先按市场价售出一些后,又降价出售.售出西瓜千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图象回答下列问题:
一水果贩子在批发市场按每千克1.8元批发了若干千克的西瓜进城出售,为了方便,他带了一些零钱备用.他先按市场价售出一些后,又降价出售.售出西瓜千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图象回答下列问题: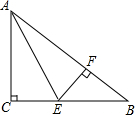 如图,在Rt△ABC中,∠C=90°,∠A的平分线交BC于点E,EF⊥AB于点F,点F恰好是AB的一个三等分点(AF>BF).
如图,在Rt△ABC中,∠C=90°,∠A的平分线交BC于点E,EF⊥AB于点F,点F恰好是AB的一个三等分点(AF>BF).