题目内容
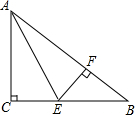如图，在Rt△ABC中，∠C=90°，∠A的平分线交BC于点E，EF⊥AB于点F，点F恰好是AB的一个三等分点（AF＞BF）．（1）求证：△ACE≌△AFE；
（2）求tan∠CAE的值．
考点：全等三角形的判定与性质,角平分线的性质,勾股定理,锐角三角函数的定义
专题：证明题
分析：（1）根据角的平分线的性质可求得CE=EF，然后根据直角三角形的判定定理求得三角形全等．
（2）由△ACE≌△AFE，得出AC=AF，CE=EF，设BF=m，则AC=2m，AF=2m，AB=3m，根据勾股定理可求得，tan∠B=
=
，CE=EF=
，在RT△ACE中，tan∠CAE=
=
=
；
（2）由△ACE≌△AFE，得出AC=AF，CE=EF，设BF=m，则AC=2m，AF=2m，AB=3m，根据勾股定理可求得，tan∠B=
| AC |
| BC |
| 2 | ||
|
| 2m | ||
|
| CE |
| AC |
| ||||
| 2m |
| ||
| 5 |
解答：（1）证明：∵AE是∠BAC的平分线，EC⊥AC，EF⊥AF，
∴CE=EF，
在Rt△ACE与Rt△AFE中，
，
∴Rt△ACE≌Rt△AFE（HL）；
（2）解：由（1）可知△ACE≌△AFE，
∴AC=AF，CE=EF，
设BF=m，则AC=2m，AF=2m，AB=3m，
∴BC=
=
=
m，
解法一：∵∠C=∠EFB=90°，
∴△EFB∽△ACB，
∴
=
，
∵CE=EF，
∴
=
=
；
解法二：∴在RT△ABC中，tan∠B=
=
=
，
在RT△EFB中，EF=BF•tan∠B=
，
∴CE=EF=
，
在RT△ACE中，tan∠CAE=
=
=
；
∴tan∠CAE=
．
∴CE=EF，
在Rt△ACE与Rt△AFE中，
|
∴Rt△ACE≌Rt△AFE（HL）；
（2）解：由（1）可知△ACE≌△AFE，
∴AC=AF，CE=EF，
设BF=m，则AC=2m，AF=2m，AB=3m，
∴BC=
| AB2-AC2 |
| 9m2-4m2 |
| 5 |
解法一：∵∠C=∠EFB=90°，
∴△EFB∽△ACB，
∴
| EF |
| AC |
| FB |
| BC |
∵CE=EF，
∴
| CE |
| AC |
| m | ||
|
| ||
| 5 |
解法二：∴在RT△ABC中，tan∠B=
| AC |
| BC |
| 2m | ||
|
| 2 | ||
|
在RT△EFB中，EF=BF•tan∠B=
| 2m | ||
|
∴CE=EF=
| 2 m | ||
|
在RT△ACE中，tan∠CAE=
| CE |
| AC |
| ||||
| 2m |
| ||
| 5 |
∴tan∠CAE=
| ||
| 5 |
点评：本题考查了直角三角形的判定、性质和利用三角函数解直角三角形，根据已知条件表示出线段的值是解本题的关键．
练习册系列答案
相关题目
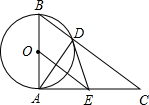如图，已知⊙O的直径为AB，AC⊥AB于点A，BC与⊙O相交于点D，在AC上取一点E，使得ED=EA．
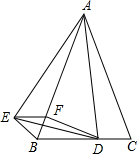如图，已知△ABC是等腰三角形，顶角∠BAC=α（α＜60°），D是BC边上的一点，连接AD，线段AD绕点A顺时针旋转α到AE，过点E作BC的平行线，交AB于点F，连接DE，BE，DF．
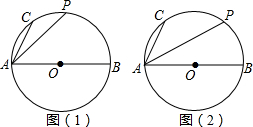如图，AB是⊙O的直径，C，P是
