题目内容
 一般地,如果在一次实验中,结果落在区域D中每一个点都是等可能的,用A表示“实验结果落在D中的某个小区域M中”这个事件,那么事件A发生的概率PA=
一般地,如果在一次实验中,结果落在区域D中每一个点都是等可能的,用A表示“实验结果落在D中的某个小区域M中”这个事件,那么事件A发生的概率PA=| M |
| D |
考点:三角形的内切圆与内心,等边三角形的性质,几何概率
专题:几何图形问题
分析:利用等边三角形以及其内切圆的性质以及锐角三角函数关系得出DO,DC的长,进而得出△ABC的高,再利用圆以及三角形面积公式求出即可.
解答: 解:连接CO,DO,
解:连接CO,DO,
由题意可得:OD⊥BC,∠OCD=30°,设BC=2x,
则CD=x,故
=tan30°,
∴DO=DCtan30°=
,
∴S圆O=π(
x)2=
,
△ABC的高为:2x•sin60°=
x,
∴S△ABC=
×2x×
x=
x2,
∴则该点落在△ABC内切圆中的概率是:
=
.
故答案为:
π.
 解:连接CO,DO,
解:连接CO,DO,由题意可得:OD⊥BC,∠OCD=30°,设BC=2x,
则CD=x,故
| DO |
| DC |
∴DO=DCtan30°=
| ||
| 3 |
∴S圆O=π(
| ||
| 3 |
| πx2 |
| 3 |
△ABC的高为:2x•sin60°=
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 3 |
| 3 |
∴则该点落在△ABC内切圆中的概率是:
| ||
|
| ||
| 9 |
故答案为:
| ||
| 9 |
点评:此题主要考查了几何概率以及三角形内切圆的性质以及等边三角形的性质等知识,得出等边三角形与内切圆的关系是解题关键.

练习册系列答案
相关题目
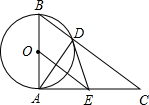 如图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.
如图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.