题目内容
7.如图,在平面直角坐标系xOy中,一次函数y=-$\frac{\sqrt{3}}{3}$x+1的图象与x轴、y轴分别交于点A、B,把Rt△AOB绕点A顺时针旋转角α(30°<α<180°),得到△AO′B′.(1)当α=60°时,判断点B是否在直线O′B′上,并说明理由;
(2)连接OO′,设OO′与AB交于点D,当α为何值时,四边形ADO′B′是平行四边形?请说明理由.

分析 (1)首先证明∠BAO=30°,再求出直线O′B′的解析式即可解决问题.
(2)如图2中,当α=120°时,四边形ADO′B′是平行四边形.只要证明∠DAO′=∠AO′B′=90°,∠O′AO=∠O′AB′=30°,即可解决问题.
解答 解;(1)如图1中,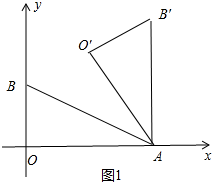
∵一次函数y=-$\frac{\sqrt{3}}{3}$x+1的图象与x轴、y轴分别交于点A、B,
∴A($\sqrt{3}$,0),B(0,1),
∴tan∠BAO=$\frac{\sqrt{3}}{3}$,
∴∠BAO=30°,AB=2OB=2,
∵旋转角为60°,
∴B′($\sqrt{3}$,2),O′($\frac{\sqrt{3}}{2}$,$\frac{3}{2}$),
设直线O′B′解析式为y=kx+b,
∴$\left\{\begin{array}{l}{\sqrt{3}k+b=2}\\{\frac{\sqrt{3}}{2}k+b=\frac{3}{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{\sqrt{3}}{3}}\\{b=1}\end{array}\right.$,
∴直线O′B′的解析式为y=$\frac{\sqrt{3}}{3}$x+1,
∵x=0时,y=1,
∴点B(0,1)在直线O′B′上.
(2)如图2中,当α=120°时,四边形ADO′B′是平行四边形.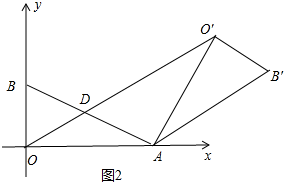
理由:∵AO=AO′,∠OAO′=120°,∠BAO=30°,
∴∠DAO′=∠AO′B′=90°,∠O′AO=∠O′AB′=30°,
∴AD∥O′B′,DO′∥AB′,
∴四边形ADO′B′是平行四边形.
点评 本题考查一次函数图象上的点的特征、平行四边形的性质和判定、旋转变换等知识,解题的关键是利用性质不变性解决问题,属于中考常考题型.

 名校课堂系列答案
名校课堂系列答案| A. | x1=x2=4 | B. | x1=x2=2$\sqrt{2}$ | ||
| C. | x1=x2=-2$\sqrt{2}$ | D. | x1=x2=2$\sqrt{2}$或x1=x2=-2$\sqrt{2}$ |
| A. | x-2y | B. | x+2y | C. | x-2y-1 | D. | x-2y+1 |
| A. | 23 | B. | 24 | C. | 25 | D. | 26 |
| A. |  | B. |  | C. |  | D. |  |