题目内容
5.已知A(-1,2),B(3,1),点P在x轴上,则AP+BP的最小值为5.分析 先求出点B关于x轴的对称点C的坐标,连接AC交x轴于P,此时PA+PB最小,根据勾股定理即可得到结论.
解答  解:作点B(3,1)关于x轴对称点C,
解:作点B(3,1)关于x轴对称点C,
则C(3,-1),
连接AC交x轴于P,
则AC=PA+PB的最小值,
∴AC=$\sqrt{(-1-3)^{2}+(2+1)^{2}}$=5,
∴AP+BP的最小值为5,
故答案为:5.
点评 本题考查的是轴对称-最短路线问题以及勾股定理的运用,熟知“两点之间线段最短”是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.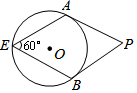 如图,PA、PB是⊙O的切线,切点分别是A、B,如果∠E=60°,那么∠P等于( )
如图,PA、PB是⊙O的切线,切点分别是A、B,如果∠E=60°,那么∠P等于( )
 如图,PA、PB是⊙O的切线,切点分别是A、B,如果∠E=60°,那么∠P等于( )
如图,PA、PB是⊙O的切线,切点分别是A、B,如果∠E=60°,那么∠P等于( )| A. | 60° | B. | 90° | C. | 120° | D. | 150° |
20.若a≥0,则$\sqrt{4{a}^{2}}$的算术平方根是( )
| A. | 2a | B. | ±2a | C. | $\sqrt{2a}$ | D. | |2a| |
17. 如图中主三视图对应的三棱柱是( )
如图中主三视图对应的三棱柱是( )
 如图中主三视图对应的三棱柱是( )
如图中主三视图对应的三棱柱是( )| A. |  | B. |  | C. |  | D. |  |
15.-2017的绝对值是( )
| A. | 2017 | B. | $\frac{1}{2017}$ | C. | -2017 | D. | -$\frac{1}{2017}$ |
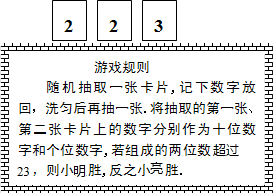 三张背面相同的卡片如图所示,将卡片洗匀后,背面朝上放置在桌面上.小明和小亮用这三张卡片做游戏,游戏规则如图所示,你认为这个游戏公平吗?请列表或画树状图说明理由.
三张背面相同的卡片如图所示,将卡片洗匀后,背面朝上放置在桌面上.小明和小亮用这三张卡片做游戏,游戏规则如图所示,你认为这个游戏公平吗?请列表或画树状图说明理由.