题目内容
3. 如图,在一次户外研学活动中,老师带领学生去测一条东西流向的河流的宽度(把河两岸看做平行线,河宽即两岸之间的垂线段的长度).某同学在河南岸A处观测到河对岸水边有一棵树P,测得P在A北偏东60°方向上,沿河岸向东前行20米到达B处,测得P在B北偏东45°方向上.求河宽(结果保留一位小数.$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).
如图,在一次户外研学活动中,老师带领学生去测一条东西流向的河流的宽度(把河两岸看做平行线,河宽即两岸之间的垂线段的长度).某同学在河南岸A处观测到河对岸水边有一棵树P,测得P在A北偏东60°方向上,沿河岸向东前行20米到达B处,测得P在B北偏东45°方向上.求河宽(结果保留一位小数.$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).
分析 过P作PC⊥AB于点C,根据题意得到∠PAC=30°,∠PBC=45°,根据正切的定义得到AC=$\sqrt{3}$PC,根据题意列方程,解方程即可.
解答 解:过P作PC⊥AB于点C,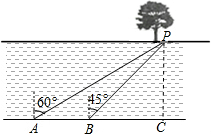
∴∠ACP=90°.
由题意可知,∠PAC=30°,∠PBC=45°.
∴∠BPC=45°.
∴BC=PC.
在Rt△ACP中,$AC=\frac{PC}{tan∠PAC}=\sqrt{3}PC$.
∵AB=20,
∴$20+PC=AC=\sqrt{3}PC$.
∴$PC=\frac{20}{{\sqrt{3}-1}}$≈27.3.
答:河流宽度约为27.3米.
点评 本题考查的是解直角三角形的应用-方向角问题,正确作出辅助线、熟记锐角三角函数的定义、正确标注方向角是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.下列计算正确的是( )
| A. | x2•x3=x5 | B. | x2+x3=2x5 | C. | 2x-3x=-1 | D. | (2x)3=2x3 |
18. 如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,则sinA的值是( )
如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,则sinA的值是( )
 如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,则sinA的值是( )
如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,则sinA的值是( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
12. 已知函数y=ax2+bx+c的图象如图所示,那么能ax2+bx+c=0的解是( )
已知函数y=ax2+bx+c的图象如图所示,那么能ax2+bx+c=0的解是( )
 已知函数y=ax2+bx+c的图象如图所示,那么能ax2+bx+c=0的解是( )
已知函数y=ax2+bx+c的图象如图所示,那么能ax2+bx+c=0的解是( )| A. | -3,-1 | B. | -3,0 | C. | -3 | D. | 3 |

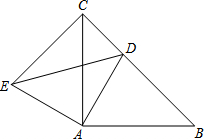 已知:如图,等腰△ABC,AB=AC,点D为△ABC的BC边上一点,连接AD,将线段AD旋转至AE,使得∠DAE=∠BAC,连接CE.
已知:如图,等腰△ABC,AB=AC,点D为△ABC的BC边上一点,连接AD,将线段AD旋转至AE,使得∠DAE=∠BAC,连接CE. 如图,在平面直角坐标系中,每个小正方形的边长为1,△ABC各顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
如图,在平面直角坐标系中,每个小正方形的边长为1,△ABC各顶点都在格点上,结合所给的平面直角坐标系解答下列问题: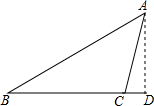 如图,在△ABC中,∠B=30°,BC=40cm,过点A作AD⊥BC,垂足为D,∠ACD=75°.
如图,在△ABC中,∠B=30°,BC=40cm,过点A作AD⊥BC,垂足为D,∠ACD=75°.