题目内容
 如图,已知在△ABC中,∠B=45°,∠C=60°,AD⊥BC于D,BC=10,则AD=
如图,已知在△ABC中,∠B=45°,∠C=60°,AD⊥BC于D,BC=10,则AD=考点:勾股定理,含30度角的直角三角形,等腰直角三角形
专题:
分析:设BD=x,则CD=10-x,根据∠B=45°,AD⊥BC得出AD=BD=x,再由∠C=60°得出∠CAD=30°,故AC=2CD=20-2x,再根据勾股定理即可得出x的值.
解答:解:∵BC=10,
∴设BD=x,则CD=10-x.
∵∠B=45°,AD⊥BC,
∴AD=BD=x.
∵∠C=60°,
∴∠CAD=30°,
∴AC=2CD=20-2x.
在Rt△ACD中,
∵AD2+CD2=AC2,即x2+(10-x)2=(20-2x)2,
解得x=10(
-1),即AD=10(
-1).
故答案为:10(
-1).
∴设BD=x,则CD=10-x.
∵∠B=45°,AD⊥BC,
∴AD=BD=x.
∵∠C=60°,
∴∠CAD=30°,
∴AC=2CD=20-2x.
在Rt△ACD中,
∵AD2+CD2=AC2,即x2+(10-x)2=(20-2x)2,
解得x=10(
| 3 |
| 3 |
故答案为:10(
| 3 |
点评:本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,AB∥CD,∠1=102°,求∠2、∠3、∠4、∠5的度数,并说明根据.
如图,AB∥CD,∠1=102°,求∠2、∠3、∠4、∠5的度数,并说明根据.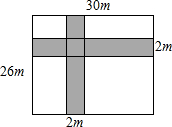 邻居李大叔在自家后院种了一块长30m,宽26m的长方形菜地,为行走方便,准备修筑两条横竖方向互相垂直的小路如图所示,路宽2m,请你帮助计算一下种植蔬菜的面积.
邻居李大叔在自家后院种了一块长30m,宽26m的长方形菜地,为行走方便,准备修筑两条横竖方向互相垂直的小路如图所示,路宽2m,请你帮助计算一下种植蔬菜的面积. 四边形ABCD中,∠B=60°,∠BCD=100°,∠D=70°,且M、N两点分别为△ABC及△ACD的内心,则∠MAN的度数为
四边形ABCD中,∠B=60°,∠BCD=100°,∠D=70°,且M、N两点分别为△ABC及△ACD的内心,则∠MAN的度数为