题目内容
已知△ABC中∠A：∠B：∠C=2：3：5，则∠B的度数为 ．
考点：三角形内角和定理
专题：
分析：设∠A=2x，∠B=3x，∠C=5x，再根据∠A+∠B+∠C=180°求出x的值，进而可得出结论．
解答：解：∵△ABC中∠A：∠B：∠C=2：3：5，
∴设∠A=2x，∠B=3x，∠C=5x．
∵∠A+∠B+∠C=180°，
∴2x+3x+5x=180°，解得x=18°，
∴∠B=3x=54°．
故答案为：54°．
∴设∠A=2x，∠B=3x，∠C=5x．
∵∠A+∠B+∠C=180°，
∴2x+3x+5x=180°，解得x=18°，
∴∠B=3x=54°．
故答案为：54°．
点评：本题考查的是三角形内角和定理，熟知三角形内角和是180°是解答此题的关键．
练习册系列答案
相关题目
若a，b为实数，且b=
+4，则a+b的值为（ ）
| ||||
| a+7 |
| A、±1 | B、4 | C、3或5 | D、5 |
我们知道“在三角行每一顶点处个取一个外角，它们的和就是这个三角形的外角和”．
在△ABC中，AB=3，BC=4，∠ABC=120°，求AC的长．
如图，已知在△ABC中，∠B=45°，∠C=60°，AD⊥BC于D，BC=10，则AD=
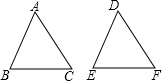如图，在△ABC与△DEF中，已有条件AB=DE，∠B=∠E，还需添加一个条件才能使△ABC≌△DEF，能添加的一个条件是（ ）| A、AC=DF |
| B、BC=DF |
| C、∠A=∠F |
| D、BC=EF |
如图，已知∠C=90°，⊙O是Rt△ABC的内切圆，AB与⊙O相切于D，AO的延长线交BC于E．证明：AD•AE=AO•AC．