题目内容
甲乙两个人进行50m往返跑,他们从50m跑道的起点同时同方向出发匀速来回跑,甲的速度为5m/s,乙的速度为2m/s,在50跑道两端转身的时间忽略不计.求:
(1)他们出发后第一次相遇需要多少时间?
(2)甲第一次从后面追上乙用了多少时间?
(3)6分钟内甲从后面追上乙共多少次?第n次甲从后面追上乙时,甲已经跑了多少路程?
(1)他们出发后第一次相遇需要多少时间?
(2)甲第一次从后面追上乙用了多少时间?
(3)6分钟内甲从后面追上乙共多少次?第n次甲从后面追上乙时,甲已经跑了多少路程?
考点:一元一次方程的应用
专题:应用题
分析:(1)甲跑50m折返后回来与乙的相遇为第一次相遇,两人跑的路程和是100m,若他们出发后第一次相遇需要xs,则(5+2)x=50•2,然后解方程;
(2)设甲第一次从后面追上乙用了ys,甲要第一次从后面追上乙,则必须要比乙多跑100m,于是利用他们的路程差列方程(5-2)y=50×2,然后解方程;
(3)用360s除以甲第一次从后面追上乙所用的时间
s,取整数得到6分钟内甲从后面追上乙的总次数;先确定第n次甲从后面追上乙所用的时间为
n,然后乘以甲的速度即可得到甲已经跑的路程.
(2)设甲第一次从后面追上乙用了ys,甲要第一次从后面追上乙,则必须要比乙多跑100m,于是利用他们的路程差列方程(5-2)y=50×2,然后解方程;
(3)用360s除以甲第一次从后面追上乙所用的时间
| 100 |
| 3 |
| 100 |
| 3 |
解答:解:(1)设他们出发后第一次相遇需要xs,
根据题意得:(5+2)x=50•2,解得x=
(s),
答:他们出发后第一次相遇需要
s;
(2)设甲第一次从后面追上乙用了ys,此时甲比乙要多跑50m×2=100m,
根据题意得:(5-2)y=50×2,解得y=
(s),
答:甲第一次从后面追上乙用了
s;
(3)6×60÷
=10.8,取整数10次,即6分钟内甲从后面追上乙共10次;5•
•n=
n(m).
答:6分钟内甲从后面追上乙共10次;第n次甲从后面追上乙时,甲已经跑了
n米.
根据题意得:(5+2)x=50•2,解得x=
| 100 |
| 7 |
答:他们出发后第一次相遇需要
| 100 |
| 7 |
(2)设甲第一次从后面追上乙用了ys,此时甲比乙要多跑50m×2=100m,
根据题意得:(5-2)y=50×2,解得y=
| 100 |
| 3 |
答:甲第一次从后面追上乙用了
| 100 |
| 3 |
(3)6×60÷
| 100 |
| 3 |
| 100 |
| 3 |
| 500 |
| 3 |
答:6分钟内甲从后面追上乙共10次;第n次甲从后面追上乙时,甲已经跑了
| 500 |
| 3 |
点评:本题考查了一元一次方程的应用:利用方程解决实际问题的基本思路如下:首先审题找出题中的未知量和所有的已知量,直接设要求的未知量或间接设一关键的未知量为x,然后用含x的式子表示相关的量,找出之间的相等关系列方程、求解、作答,即设、列、解、答.

练习册系列答案
相关题目
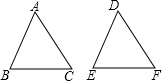 如图,在△ABC与△DEF中,已有条件AB=DE,∠B=∠E,还需添加一个条件才能使△ABC≌△DEF,能添加的一个条件是( )
如图,在△ABC与△DEF中,已有条件AB=DE,∠B=∠E,还需添加一个条件才能使△ABC≌△DEF,能添加的一个条件是( )| A、AC=DF |
| B、BC=DF |
| C、∠A=∠F |
| D、BC=EF |
 如图,已知在△ABC中,∠B=45°,∠C=60°,AD⊥BC于D,BC=10,则AD=
如图,已知在△ABC中,∠B=45°,∠C=60°,AD⊥BC于D,BC=10,则AD= 如图,∠ACB=∠AED=90°,AC=BC,AD平分∠BAC交BC于点D,若AB=9,则△DEB的周长为
如图,∠ACB=∠AED=90°,AC=BC,AD平分∠BAC交BC于点D,若AB=9,则△DEB的周长为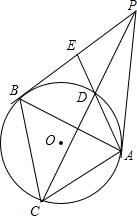 如图,点P是⊙O外的一点,PA,PB为⊙O的两条切线,E为PB的中点,连接EA,交⊙O于D点,连接PD并延长,交⊙O与C点.求证:AB=CD.
如图,点P是⊙O外的一点,PA,PB为⊙O的两条切线,E为PB的中点,连接EA,交⊙O于D点,连接PD并延长,交⊙O与C点.求证:AB=CD. 如图,已知∠C=90°,⊙O是Rt△ABC的内切圆,AB与⊙O相切于D,AO的延长线交BC于E.证明:AD•AE=AO•AC.
如图,已知∠C=90°,⊙O是Rt△ABC的内切圆,AB与⊙O相切于D,AO的延长线交BC于E.证明:AD•AE=AO•AC.