题目内容
 四边形ABCD中,∠B=60°,∠BCD=100°,∠D=70°,且M、N两点分别为△ABC及△ACD的内心,则∠MAN的度数为
四边形ABCD中,∠B=60°,∠BCD=100°,∠D=70°,且M、N两点分别为△ABC及△ACD的内心,则∠MAN的度数为考点:三角形的内切圆与内心
专题:计算题
分析:先根据四边形内角和计算出∠BAD=130°,再根据三角形内心的性质得MA平分∠BAC,NA平分∠DAC,则∠MAC=
∠BAC,∠NAC=
∠DAC,所以∠MAC+∠NAC=
(∠BAC+∠DAC),于是得到∠MAN=
∠BAD=65°.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵∠B=60°,∠BCD=100°,∠D=70°,
∴∠BAD=360°-60°-100°-70°=130°,
∵M、N两点分别为△ABC及△ACD的内心,
∴MA平分∠BAC,NA平分∠DAC,
∴∠MAC=
∠BAC,∠NAC=
∠DAC,
∴∠MAC+∠NAC=
(∠BAC+∠DAC),
即∠MAN=
∠BAD=
×130°=65°.
故答案为65°.
∴∠BAD=360°-60°-100°-70°=130°,
∵M、N两点分别为△ABC及△ACD的内心,
∴MA平分∠BAC,NA平分∠DAC,
∴∠MAC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠MAC+∠NAC=
| 1 |
| 2 |
即∠MAN=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为65°.
点评:本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,菱形ABCD,AB=17,BD=16,延长BD至点E,使AE=25,连接AE,则DE的长为( )
如图,菱形ABCD,AB=17,BD=16,延长BD至点E,使AE=25,连接AE,则DE的长为( )| A、8 | B、9 | C、11 | D、12 |
下列方程中,一元一次方程是( )
| A、2y=1 |
| B、3x-5 |
| C、3+7=10 |
| D、x2+x=1 |
 如图,已知在△ABC中,∠B=45°,∠C=60°,AD⊥BC于D,BC=10,则AD=
如图,已知在△ABC中,∠B=45°,∠C=60°,AD⊥BC于D,BC=10,则AD=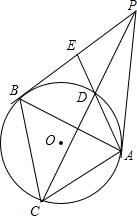 如图,点P是⊙O外的一点,PA,PB为⊙O的两条切线,E为PB的中点,连接EA,交⊙O于D点,连接PD并延长,交⊙O与C点.求证:AB=CD.
如图,点P是⊙O外的一点,PA,PB为⊙O的两条切线,E为PB的中点,连接EA,交⊙O于D点,连接PD并延长,交⊙O与C点.求证:AB=CD. 如图,已知∠C=90°,⊙O是Rt△ABC的内切圆,AB与⊙O相切于D,AO的延长线交BC于E.证明:AD•AE=AO•AC.
如图,已知∠C=90°,⊙O是Rt△ABC的内切圆,AB与⊙O相切于D,AO的延长线交BC于E.证明:AD•AE=AO•AC.