题目内容
8．
直线${y_1}=-\frac{1}{2}x-\frac{5}{2}$与直线y2=2x在同一平面直角坐标系中的图象如图所示，则不等式y1≤y2的解集为（ ）| A． | x≤-1 | B． | x≥-1 | C． | x≤-2 | D． | x≥-2 |
分析 直接根据两函数图象的交点坐标即可得出结论．
解答 解：∵由函数图象可知，当x≥-1时，直线${y_1}=-\frac{1}{2}x-\frac{5}{2}$在直线y2=2x的下方，
∴不等式y1≤y2的解集为x≥-1．
故选B．
点评 本题考查的是一次函数与一元一次不等式，能利用函数图象直接得出不等式的解集是解答此题的关键．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
1．
一次函数y1=x+b与一次函数y2=kx+4的图象交于点P（1，3），则关于x的不等式bx+2k＜0的解集是（ ）
一次函数y1=x+b与一次函数y2=kx+4的图象交于点P（1，3），则关于x的不等式bx+2k＜0的解集是（ ）| A． | x＜0 | B． | x＜3 | C． | x＞1 | D． | x＜1 |
如图所示，平行四边形ABCD的周长是14cm，对角线AC、BD相交于点O，若△AOD与△AOB的周长差是3cm，求平行四边形ABCD的相邻两边的长．
3．
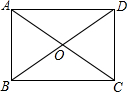如图，已知四边形ABCD中，∠BAD=∠ABC=∠BCD=90°，下列条件能使四边形ABCD成为正方形的是（ ）
如图，已知四边形ABCD中，∠BAD=∠ABC=∠BCD=90°，下列条件能使四边形ABCD成为正方形的是（ ）| A． | AC=BD | B． | AB⊥BC | C． | AD=BC | D． | AC⊥BD |
13．
如图，正方形ABCD和正方形DEFG的顶点A在y轴上，顶点D，F在x轴上，点C在DE边上，反比例函数y=$\frac{k}{x}$（k≠0）的图象经过点B、C和边EF的中点M．若S正方形ABCD=2，则正方形DEFG的面积为（ ）
如图，正方形ABCD和正方形DEFG的顶点A在y轴上，顶点D，F在x轴上，点C在DE边上，反比例函数y=$\frac{k}{x}$（k≠0）的图象经过点B、C和边EF的中点M．若S正方形ABCD=2，则正方形DEFG的面积为（ ）| A． | $\frac{10}{3}$ | B． | $\frac{32}{9}$ | C． | 4 | D． | $\frac{15}{4}$ |
20．现代互联网技术的广泛应用，促进快递行业高速发展，据调查，我市某家快递公司，今年3月份与5月份完成投递的快递总件数分别为6.3万件和8万件．设该快递公司这两个月投递总件数的月平均增长率为x，则下列方程正确的是（ ）
| A． | 6.3（1+2x）=8 | B． | 6.3（1+x）=8 | ||
| C． | 6.3（1+x）2=8 | D． | 6.3+6.3（1+x）+6.3（1+x）2=8 |