题目内容
8.已知方程组$\left\{\begin{array}{l}{2x+y=5m+6}\\{x-2y=-17}\end{array}\right.$的解为非负数,化简$\sqrt{1-4m+4{m}^{2}}$=2m-1.分析 先用m表示出x、y的值,再根据方程组的解为非负数得出m的取值范围,根据二次根式的性质把原式进行化简即可.
解答 解:解方程组$\left\{\begin{array}{l}2x+y=5m+6\\ x-2y=-17\end{array}\right.$得,$\left\{\begin{array}{l}x=2m-1\\ y=m+8\end{array}\right.$,
∵方程组的解为非负数,
∴$\left\{\begin{array}{l}2m-1≥0\\ m+8≥0\end{array}\right.$,解得m≥$\frac{1}{2}$,
∴原式=$\sqrt{(1-2m)^{2}}$=2m-1.
故答案为:2m-1.
点评 本题考查的是二元一次方程组的解,熟知二次根式具有非负性是解答此题的关键.

练习册系列答案
相关题目
16.下列各式分解因式正确的是( )
| A. | ax2-a=a(x2-1) | B. | x2+x-2=x(x+1)-2 | C. | a2b+ab2=ab(a+b) | D. | x2+1=x(x+$\frac{1}{x}$) |
13.下列事件中:①明天晴天; ②掷一枚硬币,有国徽的一面向上;③月亮绕地球转;④打开电视,正在播广告;其中不确定事件有( )
| A. | ①② | B. | ①③ | C. | ①②④ | D. | ①③④ |
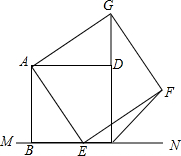 如图,已知正方形ABCD,点E是BC上一点,以AE为边作正方形AEFG.
如图,已知正方形ABCD,点E是BC上一点,以AE为边作正方形AEFG.