题目内容
20.先化简,后求值:[$\frac{1}{a-2}$+$\frac{{a}^{2}-1}{(a+2)(a-1)}$]÷($\frac{a}{a+2}$)2,其中a=2005.分析 原式先计算乘方运算,再计算除法运算,得到最简结果,把a的值代入计算即可求出值.
解答 解:原式=($\frac{1}{a-2}$+$\frac{a+1}{a+2}$)•$\frac{(a+2)^{2}}{{a}^{2}}$=$\frac{a+2+{a}^{2}-a-2}{(a+2)(a-2)}$•$\frac{(a+2)^{2}}{{a}^{2}}$=$\frac{{a}^{2}}{(a+2)(a-2)}$•$\frac{(a+2)^{2}}{{a}^{2}}$=$\frac{a+2}{a-2}$,
当a=2015时,原式=$\frac{2015+2}{2015-2}$=$\frac{2017}{2013}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
11.已知a,b,c是△ABC的三边,则关于x的方程(a+b)x2-2cx+(a+b)=0的根的情况是( )
| A. | 没有实数根 | B. | 可能有且只有一个实数根 | ||
| C. | 有两个相等的实数根 | D. | 有两个不相等的实数根 |
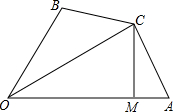 如图,在四边形OACB中,CM⊥OA于M,且CA=CB,∠OAC+∠OBC=180°,求证:
如图,在四边形OACB中,CM⊥OA于M,且CA=CB,∠OAC+∠OBC=180°,求证: 如图,在平面直角坐标系中,反比例函数y1=$\frac{k_1}{x}$(x>0)的图象与y2=$\frac{k_2}{x}$(x>0)的图象关于x轴对称,Rt△AOB的顶点A,B分别在y1=$\frac{k_1}{x}$(x>0)和y2=$\frac{k_2}{x}$(x>0)的图象上.若OB=AB,点B的纵坐标为-2,则点A的坐标为(1+$\sqrt{5}$,3-$\sqrt{5}$).
如图,在平面直角坐标系中,反比例函数y1=$\frac{k_1}{x}$(x>0)的图象与y2=$\frac{k_2}{x}$(x>0)的图象关于x轴对称,Rt△AOB的顶点A,B分别在y1=$\frac{k_1}{x}$(x>0)和y2=$\frac{k_2}{x}$(x>0)的图象上.若OB=AB,点B的纵坐标为-2,则点A的坐标为(1+$\sqrt{5}$,3-$\sqrt{5}$).