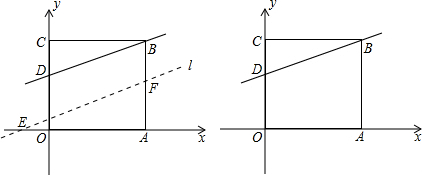题目内容
17. 如图,直线y=-x+2与x轴、y轴分别交于点A,B,点C在x轴上,∠α=75°,则点C 的坐标是( )
如图,直线y=-x+2与x轴、y轴分别交于点A,B,点C在x轴上,∠α=75°,则点C 的坐标是( )| A. | (-2$\sqrt{3}$,0) | B. | (-4,0) | C. | (-$\frac{2\sqrt{3}}{3}$,2) | D. | (-2,0) |
分析 根据题意可以求得点A、B的坐标,从而可以求得∠BCO的度数,从而可以求得OC的长度,进而求得点C的坐标.
解答 解:∵直线y=-x+2与x轴、y轴分别交于点A,B,
当x=0时,y=2,当y=0时,x=2,
∴点A(2,0),点B(0,2),
∴OA=OB=2,
∵∠AOB=90°,
∴∠ABO=∠BAO=45°,
∵∠α=75°,∠α=∠BAO+∠BAO,
∴∠BCO=30°,
∴CO=$\frac{BO}{tan∠BCO}=\frac{2}{tan30°}=\frac{2}{\frac{\sqrt{3}}{3}}=2\sqrt{3}$,
∴点C的坐标是(-2$\sqrt{3}$,0),
故选A.
点评 本题考查一次函数图象上点的坐标特征,解答此类问题的关键是明确题意,利用锐角三角函数解答.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
7. 如图,在Rt△ABC中,∠B=90°,AB=3,AC=5,点E在BC上,将△ABC沿AE折叠,使点B落在AC边上的点B′处,则BE的长为( )
如图,在Rt△ABC中,∠B=90°,AB=3,AC=5,点E在BC上,将△ABC沿AE折叠,使点B落在AC边上的点B′处,则BE的长为( )
 如图,在Rt△ABC中,∠B=90°,AB=3,AC=5,点E在BC上,将△ABC沿AE折叠,使点B落在AC边上的点B′处,则BE的长为( )
如图,在Rt△ABC中,∠B=90°,AB=3,AC=5,点E在BC上,将△ABC沿AE折叠,使点B落在AC边上的点B′处,则BE的长为( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | 2 |
6.若x:y=2:3,则下列各式不成立的是( )
| A. | $\frac{x+y}{y}$=$\frac{5}{3}$ | B. | $\frac{y-x}{y}$=$\frac{1}{3}$ | C. | $\frac{x+1}{y+1}$=$\frac{3}{4}$ | D. | $\frac{x}{2y}$=$\frac{1}{3}$ |
7.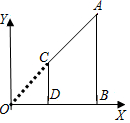 如图,AB,CD都垂直于x轴,垂足分别为B,D,若A(6,3),C(2,1),
如图,AB,CD都垂直于x轴,垂足分别为B,D,若A(6,3),C(2,1),
则△OCD与四边形ABDC的面积比为( )
 如图,AB,CD都垂直于x轴,垂足分别为B,D,若A(6,3),C(2,1),
如图,AB,CD都垂直于x轴,垂足分别为B,D,若A(6,3),C(2,1),则△OCD与四边形ABDC的面积比为( )
| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 1:8 |