题目内容
18.在直角坐标系中,O为坐标原点,点A的坐标是(2,2),若点P在x轴上,且△APO是等腰三角形,则满足条件的点P坐标是P(2,0)(-2$\sqrt{2}$,0)(2$\sqrt{2}$,0)(4,0).分析 等腰三角形要判断腰长的情况,本题可根据OA是底边、腰几种情况着手进行讨论即可得出答案.
解答 解:已知点A的坐标为(2,2),则△OAP的边OA=2$\sqrt{2}$,这条边可能是底边也可能是腰.
①当OA是底边时,点P是OA的垂直平分线与x轴的交点,这两个点的坐标是(2,0);
②当OA是腰时,当O是顶角顶点时,以O为圆心,以OA为半径作圆,与x轴的交点坐标是(2$\sqrt{2}$,0),(-2$\sqrt{2}$,0);
③当A是顶角顶点时,以A为圆心,以AO为半径作圆,与x轴的交点坐标是(4,0).
故答案为:(2,0)(-2$\sqrt{2}$,0)(2$\sqrt{2}$,0)(4,0)
点评 本题考查了等腰三角形的判定、坐标与图形性质;分情况进行讨论,能够把各种情况能够讨论全是解决本题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
8.下列结论中,不正确的是( )
| A. | 如果两条直线都和第三条直线平行,那么这两条直线也互相平行 | |
| B. | 如果两条直线都和第三条直线垂直,那么这两条直线也互相垂直 | |
| C. | 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行 | |
| D. | 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行 |
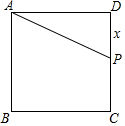 如图,正方形ABCD的边长为2,P为DC上的点(不与C,D点重合).设线段DP的长为x,求梯形ABCP的面积y关于x的函数关系式,并写出自变量x的取值范围.
如图,正方形ABCD的边长为2,P为DC上的点(不与C,D点重合).设线段DP的长为x,求梯形ABCP的面积y关于x的函数关系式,并写出自变量x的取值范围. 在如图所示的正方形网格中,每个小正方形的边长均为1,格点三角形(顶点在网格线的交点处的三角形)ABC的顶点A、C的坐标系分别为A(-4,5)、C(-1,3).
在如图所示的正方形网格中,每个小正方形的边长均为1,格点三角形(顶点在网格线的交点处的三角形)ABC的顶点A、C的坐标系分别为A(-4,5)、C(-1,3).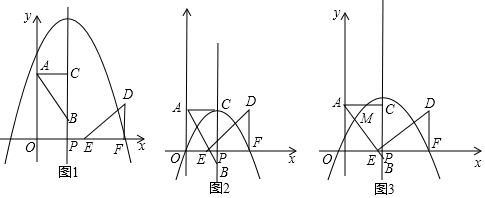
 如图,已知AC∥DE,∠A=∠E,BD=CF,求证:AB∥EF.
如图,已知AC∥DE,∠A=∠E,BD=CF,求证:AB∥EF.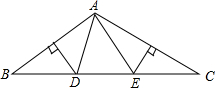 如图,在△ABC中,AB边垂直平分线交BC于点D,AC边垂直平分线交BC于点E,连接AD,AE.
如图,在△ABC中,AB边垂直平分线交BC于点D,AC边垂直平分线交BC于点E,连接AD,AE.