题目内容
12.在?ABCD中,E、F分别是边AD、BC的中点,AC分别交BE、DF于G、H,请判断下列结论:其中错误的结论是( )| A. | BE=DF | B. | AG=GH=HC | C. | EG=$\frac{1}{2}$BG | D. | S△ABE=2S△AGE |
分析 根据BF∥DE,BF=DE可证BEDF为平行四边形可得选项A正确;根据平行线等分线段定理判断B正确;根据△AGE∽△CGB可得选项C正确;由选项C可得△ABG的面积=△AGE面积×2,可得选项D错误,问题得解.
解答 解:A、∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC.
E、F分别是边AD、BC的中点,
∴BF∥DE,BF=DE.
∴四边形BEDF为平行四边形,BE=DF.故此选项正确;
B、根据平行线等分线段定理可得AG=GH=HC.故此选项正确;
C、∵AD∥BC,AE=$\frac{1}{2}$AD=$\frac{1}{2}$BC,
∴△AGE∽△CGB,AE:BC=EG:BG=1:2,
∴EG=$\frac{1}{2}$BG.故此选项正确.
D、∵BG=2EG,
∴△ABG的面积=△AGE面积×2,
∴S△ABE=3S△AGE.故此选项错误.
故选D.
点评 此题考查了平行四边形的判定及性质、相似三角形的判定及性质等知识点,难度中等,解题的关键是熟记平行四边形的各种性质以及判定方法.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
7.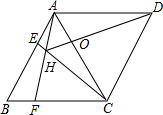 如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,连接DH交AG于点O.则下列结论①△ABF≌△CAE,②∠AHC=120°,③AH+CH=DH中,正确的是( )
如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,连接DH交AG于点O.则下列结论①△ABF≌△CAE,②∠AHC=120°,③AH+CH=DH中,正确的是( )
 如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,连接DH交AG于点O.则下列结论①△ABF≌△CAE,②∠AHC=120°,③AH+CH=DH中,正确的是( )
如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,连接DH交AG于点O.则下列结论①△ABF≌△CAE,②∠AHC=120°,③AH+CH=DH中,正确的是( )| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
17. 如图,AOE是一条直线,图中小于平角的角共有( )
如图,AOE是一条直线,图中小于平角的角共有( )
 如图,AOE是一条直线,图中小于平角的角共有( )
如图,AOE是一条直线,图中小于平角的角共有( )| A. | 4个 | B. | 8个 | C. | 9个 | D. | 10个 |
4.已知等腰三角形的两边长是5cm和6cm,则此三角形的周长是( )
| A. | 16cm | B. | 17cm | C. | 11cm | D. | 16cm或17cm |
 如图所示,D是△ABC的边AB上一点,∠B=∠1,BD=4,AD=3,则AC=$\sqrt{21}$.
如图所示,D是△ABC的边AB上一点,∠B=∠1,BD=4,AD=3,则AC=$\sqrt{21}$.