题目内容
17. 如图,点O是直线AB、CD的交点,OE⊥AB,OF⊥CD,OM是∠BOF的平分线.
如图,点O是直线AB、CD的交点,OE⊥AB,OF⊥CD,OM是∠BOF的平分线.(1)填空:
①由OM是∠BOF的平分线,可得∠FOM=∠BOM;
②若∠AOC=34°,则∠BOD=34度;
③根据同角的余角相等,可得∠EOF=∠AOC;
(2)若∠AOC=α,求∠COM.(用含α的代数式表示,并写出过程)
分析 (1)①直接利用角平分线的性质得出答案;
②直接利用对顶角的定义得出答案;
③利用同角的余角相等得出答案;
(2)首先表示出∠BOF的度数,再利用∠MOF=$\frac{1}{2}$∠BOF=45°-$\frac{1}{2}$α,进而得出答案.
解答 解:(1)①由OM是∠BOF的平分线,可得∠FOM=∠BOM;
②若∠AOC=34°,则∠BOD=34度;
③根据同角的余角相等,可得∠EOF=∠AOC;
故答案为:BOM,34,同角的余角相等;
(2)∵∠AOC=α,
∴∠BOD=∠AOC=α,
∵OF⊥CD,
∴∠BOF=90°-∠BOD=90°-α,
∵OM是∠BOF的平分线,
∴∠MOF=$\frac{1}{2}$∠BOF=45°-$\frac{1}{2}$α,
∵OF⊥CD,
∴∠COM=90°+∠MOF
=90°+45°-$\frac{1}{2}$α
=135°-$\frac{1}{2}$α.
点评 此题主要考查了垂直的定义以及角平分线的性质和角的有关计算,正确表示出∠BOM的度数是解题关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
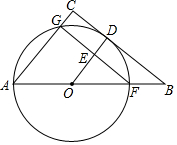 如图,在△ABC中,F是AB上一点,以AF为直径的⊙O切BC于点D,交AC于点G,AC∥OD,OD与GF交于点E.
如图,在△ABC中,F是AB上一点,以AF为直径的⊙O切BC于点D,交AC于点G,AC∥OD,OD与GF交于点E.
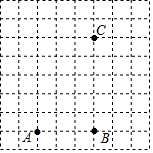 如图所示,已知点A、B、C是网格纸上的三个格点,根据要求画图或作答.
如图所示,已知点A、B、C是网格纸上的三个格点,根据要求画图或作答.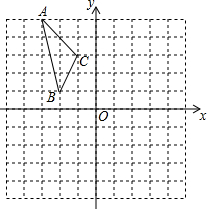 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).