题目内容
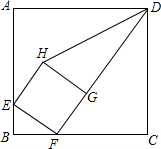 如图,在正方形ABCD中,有一个小正方形EFGH,其中顶点E,F,G分别在AB,BC,FD上.
如图,在正方形ABCD中,有一个小正方形EFGH,其中顶点E,F,G分别在AB,BC,FD上.(1)求证:△EBF∽△FCD;
(2)连接DH,如果BC=12,BF=3,求tan∠HDG的值.
考点:相似三角形的判定与性质,正方形的性质
专题:
分析:(1)根据正方形的性质可得∠B=∠C=90°,∠EFG=90°,BC=CD,GH=EF=FG,然后求出∠EFB=∠FDC,再根据有两组角对应相等的两个三角形相似证明;
(2)先求出CF,再利用勾股定理列式求出DF,然后根据相似三角形对应边成比例求出BE,再根据锐角的正切等于对边比邻边列式计算即可得解.
(2)先求出CF,再利用勾股定理列式求出DF,然后根据相似三角形对应边成比例求出BE,再根据锐角的正切等于对边比邻边列式计算即可得解.
解答:(1)证明:∵在正方形ABCD,正方形EFGH中,∠B=∠C=90°,∠EFG=90°,
∴BC=CD,GH=EF=FG.
又∵点F在BC上,点G在FD上,
∴∠DFC+∠EFB=90°,∠DFC+∠FDC=90°,
∴∠EFB=∠FDC,
又∵∠B=∠C=90°,
∴△EBF∽△FCD;
(2)解:∵BF=3,BC=CD=12,
∴CF=9,DF=
=
=15,
∵△EBF∽△FCD,
∴
=
,
∴BE=
=
=
,
∴GH=FG=EF=
=
,
∴DG=DF-FG=15-
=
,
∴tan∠HDG=
=
=
.
∴BC=CD,GH=EF=FG.
又∵点F在BC上,点G在FD上,
∴∠DFC+∠EFB=90°,∠DFC+∠FDC=90°,
∴∠EFB=∠FDC,
又∵∠B=∠C=90°,
∴△EBF∽△FCD;
(2)解:∵BF=3,BC=CD=12,
∴CF=9,DF=
| CF2+CD2 |
| 92+122 |
∵△EBF∽△FCD,
∴
| BE |
| BF |
| CF |
| CD |
∴BE=
| BF•CF |
| CD |
| 3×9 |
| 12 |
| 9 |
| 4 |
∴GH=FG=EF=
| BE2+BF2 |
| 15 |
| 4 |
∴DG=DF-FG=15-
| 15 |
| 4 |
| 45 |
| 4 |
∴tan∠HDG=
| GH |
| DG |
| ||
|
| 1 |
| 3 |
点评:本题考查了相似三角形的判定与性质,正方形的性质,勾股定理,熟记各性质以及相似三角形的判定方法是解题的关键.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案
相关题目
方程(x+1)(x-2)=x-2的解为( )
| A、x=0 |
| B、x=-1 |
| C、x1=2,x2=-1 |
| D、x1=0,x2=2 |
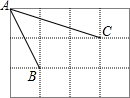 如图,在正方形网格中,小正方形的边长均为1,点A、B、C都是格点,则cos∠BAC=
如图,在正方形网格中,小正方形的边长均为1,点A、B、C都是格点,则cos∠BAC= 如图,△ABC中,点D在AB上,∠ACD=∠ABC,若AD=2,AB=6,求AC的长.
如图,△ABC中,点D在AB上,∠ACD=∠ABC,若AD=2,AB=6,求AC的长. 如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于E,交BC于D.
如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于E,交BC于D.