题目内容
19.直线AB∥CD,连接AC,点O为平面内一动点,(不在AB,CD,AC上),连接OA,OC.(1)如图,当O在直线AB,CD之间,且点O在线段AC的右侧时,求证:∠AOC=∠BAO+∠DCO;
(2)当点O在直线AB上方时,探究∠AOC,∠BAO,∠DCO之间的关系,并验证你的结论.
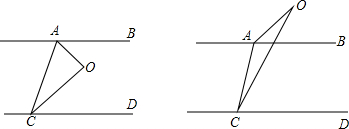
分析 (1)过点O作OE∥AB,根据平行线的性质可得出∠BAO=∠1,∠DCO=∠2,故可得出结论;
(2)先根据AB∥CD得出∠DCO=∠BFO,再由三角形外角的性质即可得出结论.
解答  (1)证明:如图1所示,
(1)证明:如图1所示,
过点O作OE∥AB,
∵AB∥CD,
∴AB∥CD∥OE,
∴∠BAO=∠1,∠DCO=∠2,
∴∠AOC=∠BAO+∠DCO;
(2)∠AOC+∠BAO=∠DCO.
证明:如图2,
∵AB∥CD,
∴∠DCO=∠BFO,
∵∠BFO△AOF的外角,
∴∠AOC+∠BAO=∠DCO.
点评 本题考查的是平行线的性质,根据题意作出平行线是解答此题的关键.

练习册系列答案
相关题目
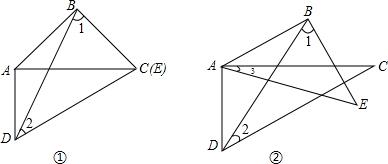
 如图,已知∠1+∠2=80°,则∠3=140°.
如图,已知∠1+∠2=80°,则∠3=140°.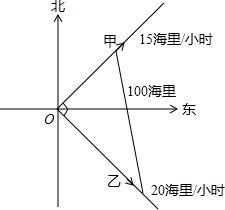 两条船同时从A港出发,一艘船的速度是15海里/时,航向是东北方向,另一艘船比它每小时快5海里,航向是东南方向,多少小时后两船相距100海里?
两条船同时从A港出发,一艘船的速度是15海里/时,航向是东北方向,另一艘船比它每小时快5海里,航向是东南方向,多少小时后两船相距100海里?