题目内容
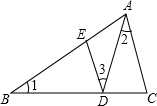如图，D、E分别是△ABC的边BC、AB上的点，△ABC，△BDE，△ACD的周长依次为m，m1，m2．（1）当∠2=∠3，BD=
| 3 |
| 5 |
| m1 |
| m |
（2）当∠1=∠2，BD=
| 3 |
| 5 |
| m2 |
| m |
（3）当∠1=∠2=∠3时，证明：
| m1+m2 |
| m |
| 5 |
| 4 |
考点：相似形综合题
专题：
分析：（1）直接利用已知得出△BDE∽△BCA，进而利用相似三角形周长比等于相似比进而得出答案；
（2）根据已知得出△ACD∽△BCA，进而得出
=
=
，求出即可；
（3）由∠2=∠3，得DE∥AC，则△BDE∽△BCA，进而得出△ACD∽△BDE∽△BCA，即可得出
=
①，
=
=
②，结合完全平方公式求出即可．
（2）根据已知得出△ACD∽△BCA，进而得出
| m2 |
| m |
| DC |
| AC |
| AC |
| BC |
（3）由∠2=∠3，得DE∥AC，则△BDE∽△BCA，进而得出△ACD∽△BDE∽△BCA，即可得出
| m1 |
| m |
| BD |
| BC |
| m2 |
| m |
| DC |
| AC |
| AC |
| BC |
解答：解：（1）∵∠2=∠3，
∴DE∥AC，
∴△BDE∽△BCA，
∴
=
，
由BD=
BC，得
=
，
即
=
；
（2）∵∠1=∠2，∠C是公共角，
∴△ACD∽△BCA，
∴
=
=
，
∴（
）2=
×
=
，
由BD=
BC，得DC=
BC，
∴（
）2=
；
（3）证法一：∵∠2=∠3，
∴DE∥AC，
∴△BDE∽△BCA；
∵∠1=∠2，∠C是公共角，
∴△ACD∽△BCA，
∴△ACD∽△BDE∽△BCA．
∴
=
①
=
=
，②
由②得，（
）2=
×
=
=
=1-
=1-
，
∴
=1-（
）2．
=
+
=1-（
）2+
，
=-（
）2+
+1=-（
-
）2+
，
∵-（
-
）2≤0，
∴
≤
．
证法二：由∠2=∠3，得AC∥DE，∴△BCA∽△BDE．
∵∠1=∠2，∠C是公共角，
∴△BCA∽△ACD，
∴△BCA∽△BDE∽△ACD．
∵△ABC，△EBD，△ADC的周长为m，m 1 ，m2，
∴相似比为m：m 1 ：m2，
∴BC：BD：AC=m：m1：m2，
设
=
=
=k，
则BC=mk，BD=m1k，AC=m2k．
CD=BC-BD=（m-m1）k，由
=
，得
=
，
等式左边的分子、分母同除以m，
得
=
，
设
=x，
=y，
则
=x，1-y=x2，y=1-x2，
=
+
=x+y=x+1-x2，
=-x2+x+1=-（x-
）2+
，
当x=
时，
取得最大值
，
∴
≤
．
证法三：证明：由∠2=∠3，得DE∥AC，
∴△EBD∽△ABC．设相似比为k，由题意知，
0＜k＜1．则
=
=
=
=k．
∵∠2=∠1，∠C是公共角，∴△DAC∽△ABC，
∴
=
=
=
．
在△ABC中，设AB=x，AC=y，BC=z，
由
=k，得BD=kBC=k•z，CD=BC-BD=z-kz．
由
=k，得DE=kAC=ky．
由△ABC∽△DAC，得
=
，
得
=
，∴y2=z2（1-k），
∵0＜k＜1，∴1-k＞0，∴y=z
，
∴
=
+
=
+
=
=
=k+
．
设
=n，
则1-k=n2，k=1-n2，
∴
=1-n2+n
=-n2+n+1
=-（n-
）2+
，
当n=
时，
取得最大值
，
∴
≤
．
∴DE∥AC，
∴△BDE∽△BCA，
∴
| m1 |
| m |
| BD |
| BC |
由BD=
| 3 |
| 5 |
| BD |
| BC |
| 3 |
| 5 |
即
| m1 |
| m |
| 3 |
| 5 |
（2）∵∠1=∠2，∠C是公共角，
∴△ACD∽△BCA，
∴
| m2 |
| m |
| DC |
| AC |
| AC |
| BC |
∴（
| m2 |
| m |
| DC |
| AC |
| AC |
| BC |
| DC |
| BC |
由BD=
| 3 |
| 5 |
| 2 |
| 5 |
∴（
| m2 |
| m |
| 2 |
| 5 |
（3）证法一：∵∠2=∠3，
∴DE∥AC，
∴△BDE∽△BCA；
∵∠1=∠2，∠C是公共角，
∴△ACD∽△BCA，
∴△ACD∽△BDE∽△BCA．
∴
| m1 |
| m |
| BD |
| BC |
| m2 |
| m |
| DC |
| AC |
| AC |
| BC |
由②得，（
| m2 |
| m |
| DC |
| AC |
| AC |
| BC |
| DC |
| BC |
=
| BC-BD |
| BC |
| BD |
| BC |
| m1 |
| m |
∴
| m1 |
| m |
| m2 |
| m |
| m1+m2 |
| m |
| m1 |
| m |
| m2 |
| m |
| m2 |
| m |
| m2 |
| m |
=-（
| m2 |
| m |
| m2 |
| m |
| m2 |
| m |
| 1 |
| 2 |
| 5 |
| 4 |
∵-（
| m2 |
| m |
| 1 |
| 2 |
∴
| m1+m2 |
| m |
| 5 |
| 4 |
证法二：由∠2=∠3，得AC∥DE，∴△BCA∽△BDE．
∵∠1=∠2，∠C是公共角，
∴△BCA∽△ACD，
∴△BCA∽△BDE∽△ACD．
∵△ABC，△EBD，△ADC的周长为m，m 1 ，m2，
∴相似比为m：m 1 ：m2，
∴BC：BD：AC=m：m1：m2，
设
| BC |
| m |
| BD |
| m1 |
| AC |
| m2 |
则BC=mk，BD=m1k，AC=m2k．
CD=BC-BD=（m-m1）k，由
| CD |
| AC |
| AC |
| BC |
| m-m1 |
| m2 |
| m2 |
| m |
等式左边的分子、分母同除以m，
得
1-
| ||
|
| m2 |
| m |
设
| m2 |
| m |
| m1 |
| m |
则
| 1-y |
| x |
| m1+m2 |
| m |
| m1 |
| m |
| m2 |
| m |
=-x2+x+1=-（x-
| 1 |
| 2 |
| 5 |
| 4 |
当x=
| 1 |
| 2 |
| m1+m2 |
| m |
| 5 |
| 4 |
∴
| m1+m2 |
| m |
| 5 |
| 4 |
证法三：证明：由∠2=∠3，得DE∥AC，
∴△EBD∽△ABC．设相似比为k，由题意知，
0＜k＜1．则
| m1 |
| m |
| DE |
| AC |
| BE |
| AB |
| BD |
| BC |
∵∠2=∠1，∠C是公共角，∴△DAC∽△ABC，
∴
| m2 |
| m |
| DC |
| AC |
| AD |
| AB |
| AC |
| BC |
在△ABC中，设AB=x，AC=y，BC=z，
由
| BD |
| BC |
由
| DE |
| AC |
由△ABC∽△DAC，得
| AC |
| BC |
| DC |
| AC |
得
| y |
| z |
| z-kz |
| y |
∵0＜k＜1，∴1-k＞0，∴y=z
| 1-k |
∴
| m1+m2 |
| m |
| m1 |
| m |
| m2 |
| m |
| DE |
| AC |
| DC |
| AC |
=
| ky+(z-kz) |
| y |
k•z
| ||
z
|
| 1-k |
设
| 1-k |
则1-k=n2，k=1-n2，
∴
| m1+m2 |
| m |
=1-n2+n
=-n2+n+1
=-（n-
| 1 |
| 2 |
| 5 |
| 4 |
当n=
| 1 |
| 2 |
| m1+m2 |
| m |
| 5 |
| 4 |
∴
| m1+m2 |
| m |
| 5 |
| 4 |
点评：此题主要考查了相似三角形的判定与性质以及相似比与周长比的关系等知识，熟练应用相似三角形的判定与性质是解题关键．
练习册系列答案
教材全解字词句篇系列答案
相关题目
