��Ŀ����
��ͼ��ֱ������ABCO������OA��OC����������������ϣ�BC��x�ᣬOA=OC=4����ֱ��x=1Ϊ�Գ���������߹�A��B��C���㣮
��1����������ߵĺ�������ʽ��
��2����ֱ֪��l�Ľ���ʽΪy=x+m������x�ύ�ڵ�G��������ABCO��һ����ȡ��P��
�ٵ�m=0ʱ����ͼ1����P�������߶Գ�����BC�Ľ��㣬����P��PH��ֱ��l�ڵ�H������OP�������OPH�������
�ڵ�m=-3ʱ������P�ֱ���x�ᡢֱ��l�Ĵ��ߣ�����Ϊ��E��F���Ƿ���������ĵ�P��ʹ��P��E��FΪ������������ǵ��������Σ������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�

��1����������ߵĺ�������ʽ��
��2����ֱ֪��l�Ľ���ʽΪy=x+m������x�ύ�ڵ�G��������ABCO��һ����ȡ��P��
�ٵ�m=0ʱ����ͼ1����P�������߶Գ�����BC�Ľ��㣬����P��PH��ֱ��l�ڵ�H������OP�������OPH�������
�ڵ�m=-3ʱ������P�ֱ���x�ᡢֱ��l�Ĵ��ߣ�����Ϊ��E��F���Ƿ���������ĵ�P��ʹ��P��E��FΪ������������ǵ��������Σ������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�

���㣺���κ����ۺ���
ר�⣺ѹ����
��������1�����ô���ϵ������������ߵĽ���ʽ��
��2�������ͼ1���������ߣ����ù�ϵʽS��OPH=S��OMH-S��OMP��⣻
�ڱ����漰���ӵķ������ۣ����ͼ2��ʾ�����ڵ�P������OC��BC��BK��AK��OA�ϣ������������α��������������Σ������������Ĺ��̱Ƚϸ��ӣ���Ҫ����ϸ�¡�����ȫ�森
��2�������ͼ1���������ߣ����ù�ϵʽS��OPH=S��OMH-S��OMP��⣻
�ڱ����漰���ӵķ������ۣ����ͼ2��ʾ�����ڵ�P������OC��BC��BK��AK��OA�ϣ������������α��������������Σ������������Ĺ��̱Ƚϸ��ӣ���Ҫ����ϸ�¡�����ȫ�森
����⣺��1��������ã�A��4��0����C��0��4�����Գ���Ϊx=1��
�������ߵĽ���ʽΪy=ax2+bx+c�����У�
��
���
��
�������ߵĺ�������ʽΪ��y=-
x2+x+4��
��2���ٵ�m=0ʱ��ֱ��l��y=x��
�������߶Գ���Ϊx=1��
��CP=1��
���ͼ1���ӳ�HP��y���ڵ�M�����OMH����CMP��Ϊ����ֱ�������Σ�

��CM=CP=1��
��OM=OC+CM=5��
S��OPH=S��OMH-S��OMP=
��
OM��2-
OM•CP=
����
��5��2-
��5��1=
-
=
��
��S��OPH=
��
�ڵ�m=-3ʱ��ֱ��l��y=x-3��
��ֱ��l��x�ᡢy�ύ�ڵ�G����D����G��3��0����D��0��-3����
����������������ĵ�P��
a������P��OC����ʱ�����ͼ2-1��ʾ����ʱ��E���O�غϣ�
��PE=a��0��a��4����
��PD=3+a��PF=
PD=
��3+a����
����F��FN��y���ڵ�N����FN=PN=
PF����EN=|PN-PE|=|
PF-PE|��
��Rt��EFN�У��ɹ��ɶ����ã�EF=
=
��
��PE=PF����a=
��3+a�������a=3��
+1����4���ʴ������β����ڣ�
��PF=EF����PF=
��������PE=
PF����a=3+a�����������ʴ������β����ڣ�
��PE=EF����PE=
��������PF=
PE����
��3+a��=
a�����a=3��
��P1��0��3����

b������P��BC����ʱ�����ͼ2-2��ʾ����ʱPE=4��
��PE=PF�����PΪ��OGD�Ľ�ƽ������BC�Ľ��㣬��GE=GF������F�ֱ���FH��PE�ڵ�H��FK��x���ڵ�K��
�ߡ�OGD=135�㣬
���EPF=45�㣬����PHFΪ����ֱ�������Σ�
��GE=GF=t����GK=FK=EH=
t��
��PH=HF=EK=EG+GK=t+
t��
��PE=PH+EH=t+
t+
t=4��
���t=4
-4��
��OE=3-t=7-4
��
��P2��7-4
��4��
c����A��4��0����B��2��4����
������ֱ��AB����ʽΪ��y=-2x+8��
����y=-2x+8��y=x-3�����x=
��y=
��
��ֱ��BA��ֱ��l���ڵ�K����K��
��
����
����P���߶�BK��ʱ�����ͼ2-3��ʾ��
��P��a��8-2a����2��a��
������Q��a��a-3����
��PE=8-2a��PQ=11-3a��
��PF=
��11-3a����
��a��ͬ��������ã�EF=
��
��PE=PF����8-2a=
��11-3a�������a=1-2
��0���ʴ������β����ڣ�
��PF=EF����PF=
��������PE=
PF����8-2a=
•
��11-3a�������a=3��������������ʱP3��3��2����
��PE=EF����PE=
��������PF=
PE����
��11-3a��=
��8-2a�������a=5��
���ʴ������β����ڣ�

d������P���߶�KA��ʱ�����ͼ2-4��ʾ��
��PE��PF�н�Ϊ135�㣬
��ֻ������PE=PF������
���P�ڡ�KGA��ƽ�����ϣ�
��˽�ƽ������y�ύ�ڵ�M������M��MN��ֱ��l�ڵ�N����OM=MN��MD=
MN��
��OD=OM+MD=3�������M��0��3-3
����
����ΪG��3��0����
�����ֱ��MG�Ľ���ʽΪ��y=��
-1��x+3-3
��
����ֱ��MG��y=��
-1��x+3-3
��ֱ��AB��y=-2x+8��
����ã�P4��1+2
��6-4
����
e������P��OA����ʱ����ʱPE=0�����������β����ڣ�
�����������������������ĵ�P����P����Ϊ����0��3������3��2������7-4
��4������1+2
��6-4
����
�������ߵĽ���ʽΪy=ax2+bx+c�����У�
|
���
|
�������ߵĺ�������ʽΪ��y=-
| 1 |
| 2 |
��2���ٵ�m=0ʱ��ֱ��l��y=x��
�������߶Գ���Ϊx=1��
��CP=1��
���ͼ1���ӳ�HP��y���ڵ�M�����OMH����CMP��Ϊ����ֱ�������Σ�

��CM=CP=1��
��OM=OC+CM=5��
S��OPH=S��OMH-S��OMP=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 25 |
| 4 |
| 5 |
| 2 |
| 15 |
| 4 |
��S��OPH=
| 15 |
| 4 |
�ڵ�m=-3ʱ��ֱ��l��y=x-3��
��ֱ��l��x�ᡢy�ύ�ڵ�G����D����G��3��0����D��0��-3����
����������������ĵ�P��
a������P��OC����ʱ�����ͼ2-1��ʾ����ʱ��E���O�غϣ�
��PE=a��0��a��4����
��PD=3+a��PF=
| ||
| 2 |
| ||
| 2 |
����F��FN��y���ڵ�N����FN=PN=
| ||
| 2 |
| ||
| 2 |
��Rt��EFN�У��ɹ��ɶ����ã�EF=
| EN2+FN2 |
PE2-
|
��PE=PF����a=
| ||
| 2 |
| 2 |
��PF=EF����PF=
PE2-
|
| 2 |
��PE=EF����PE=
PE2-
|
| 2 |
| ||
| 2 |
| 2 |
��P1��0��3����

b������P��BC����ʱ�����ͼ2-2��ʾ����ʱPE=4��
��PE=PF�����PΪ��OGD�Ľ�ƽ������BC�Ľ��㣬��GE=GF������F�ֱ���FH��PE�ڵ�H��FK��x���ڵ�K��
�ߡ�OGD=135�㣬
���EPF=45�㣬����PHFΪ����ֱ�������Σ�
��GE=GF=t����GK=FK=EH=
| ||
| 2 |
��PH=HF=EK=EG+GK=t+
| ||
| 2 |
��PE=PH+EH=t+
| ||
| 2 |
| ||
| 2 |
���t=4
| 2 |
��OE=3-t=7-4
| 2 |
��P2��7-4
| 2 |
c����A��4��0����B��2��4����
������ֱ��AB����ʽΪ��y=-2x+8��
����y=-2x+8��y=x-3�����x=
| 11 |
| 3 |
| 2 |
| 3 |
��ֱ��BA��ֱ��l���ڵ�K����K��
| 11 |
| 3 |
| 2 |
| 3 |
����P���߶�BK��ʱ�����ͼ2-3��ʾ��
��P��a��8-2a����2��a��
| 11 |
| 3 |
��PE=8-2a��PQ=11-3a��
��PF=
| ||
| 2 |
��a��ͬ��������ã�EF=
PE2-
|
��PE=PF����8-2a=
| ||
| 2 |
| 2 |
��PF=EF����PF=
PE2-
|
| 2 |
| 2 |
| ||
| 2 |
��PE=EF����PE=
PE2-
|
| 2 |
| ||
| 2 |
| 2 |
| 11 |
| 3 |

d������P���߶�KA��ʱ�����ͼ2-4��ʾ��
��PE��PF�н�Ϊ135�㣬
��ֻ������PE=PF������
���P�ڡ�KGA��ƽ�����ϣ�
��˽�ƽ������y�ύ�ڵ�M������M��MN��ֱ��l�ڵ�N����OM=MN��MD=
| 2 |
��OD=OM+MD=3�������M��0��3-3
| 2 |
����ΪG��3��0����
�����ֱ��MG�Ľ���ʽΪ��y=��
| 2 |
| 2 |
����ֱ��MG��y=��
| 2 |
| 2 |
����ã�P4��1+2
| 2 |
| 2 |
e������P��OA����ʱ����ʱPE=0�����������β����ڣ�
�����������������������ĵ�P����P����Ϊ����0��3������3��2������7-4
| 2 |
| 2 |
| 2 |
�����������Ƕ��κ���ѹ���⣬�漰���κ�����ͼ�������ʡ�����ϵ������ͼ����������ɶ�������ƽ�������ʵ�֪ʶ�㣬�ص㿼���˷������۵���ѧ˼�룮�ڣ�2���������漰���ӵķ������ۣ�ʹ��������ѶȽϴ�

��ϰ��ϵ�д�
�����Ŀ
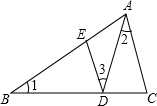 ��ͼ��D��E�ֱ��ǡ�ABC�ı�BC��AB�ϵĵ㣬��ABC����BDE����ACD���ܳ�����Ϊm��m1��m2��
��ͼ��D��E�ֱ��ǡ�ABC�ı�BC��AB�ϵĵ㣬��ABC����BDE����ACD���ܳ�����Ϊm��m1��m2��