题目内容
7.已知△ABC是锐角三角形,BA=BC,点E为AC边的中点,点D为AB边上一点,且∠ABC=∠AED=α.(1)如图1,当α=40°时,∠ADE=70°;
(2)如图2,取BC边的中点F,联结FD,将∠AED绕点E顺时针旋转适当的角度β(β<α),得到∠MEN,EM与BA的延长线交于点M,EN与FD的延长线交于点N.
①依题意补全图形;
②猜想线段EM与EN之间的数量关系,并证明你的结论.

分析 (1)根据等腰三角形的性质和三角形的内角和定理可求;
(2)①根据题意画图即可;
②首先证明EA=ED=EC,得到∠ADC=90°,然后求出∠EAM=∠EDN,易证△EAM≌△EDN,所以EM=EN.
解答 解:(1)70;
∵AB=BC,∠ABC=α=40°,
∴∠A=70°,
∵∠AED=α=40°
∴∠ADE=70°;
(2)①见右图;
②EM=EN.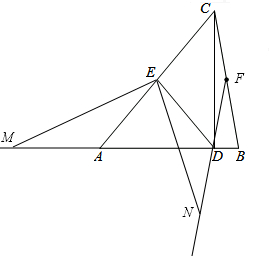
证明:∵∠ABC=∠AED=α.BA=BC,
∴∠A=∠EDA=∠ACB=90°-$\frac{α}{2}$,
∴EA=ED,
∵E是AC中点,
∴EA=EC,
∴EA=EC=ED,
∴∠ADC=90°,
∵∠EAM=180°-∠EAD=180°-(90°-$\frac{α}{2}$)=90°+$\frac{α}{2}$,
∵点F是BC中点,
∴FB=FD,
∴∠FDB=∠ABC=α,
∴∠EDN=∠EDA+∠ADN=∠EDA+∠FDB=90°-$\frac{α}{2}$+α=90°+$\frac{α}{2}$,
∴∠EAM=∠EDN,
∵∠AED绕点E顺时针旋转适当的角度,得到∠MEN,
∴∠AED=∠MEN,
∴∠AED-∠AEN=∠MEN-∠AEN,
即∠MEA=∠NED,
在△EAM和△EPN中
$\left\{\begin{array}{l}{∠EAM=∠EDN}\\{EA=ED}\\{∠MEA=∠NED}\end{array}\right.$,
∴△EAM≌△EPN(ASA),
∴EM=EN.
点评 本题主要考查了等腰三角形的性质和判定,直角三角形斜边中线等于斜边的一半,如果三角形一边中线等于这条边的一半,那么这个三角形是直角三角形,三角形内角和定理以及三角形全等的性质与判定,挖掘三角形全等的条件是解决问题的关键.

练习册系列答案
相关题目
18.在实数-0.8,2015,-$\frac{22}{7}$,$\frac{\sqrt{3}}{3}$四个数中,是无理数的是( )
| A. | -0.8 | B. | 2015 | C. | -$\frac{22}{7}$ | D. | $\frac{\sqrt{3}}{3}$ |
12.对点(x,y)的一次操作变换记为p1(x,y),定义其变换法则如下:p1(x,y)=(x+y,x-y);且规定Pn(x,y)=P1(Pn-1(x,y))(n为大于1的整数).例如:p1(1,2)=(3,-1),p2(1,2)=p1(p1(1,2))=p1(3,-1)=(2,4),p3(1,2)=p1(p2(1,2))=p1(2,4)=(6,-2).则p2014(1,-1)=( )
| A. | (0,21006) | B. | (21007,-21007) | C. | (0,-21006) | D. | (21006,-21006) |
19.-$\frac{1}{3}$的倒数是( )
| A. | -3 | B. | 3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
 如图所示,在△ABC中,AB=AC,CD垂直于BA的延长线于点D,试探究∠BAC与∠BCD之间的关系.
如图所示,在△ABC中,AB=AC,CD垂直于BA的延长线于点D,试探究∠BAC与∠BCD之间的关系.