题目内容
17. 如图所示,在△ABC中,AB=AC,CD垂直于BA的延长线于点D,试探究∠BAC与∠BCD之间的关系.
如图所示,在△ABC中,AB=AC,CD垂直于BA的延长线于点D,试探究∠BAC与∠BCD之间的关系.
分析 首先根据CD⊥AD,可得∠CDA=90°,所以∠DAC+∠DCA=180°-90°=90°;然后根据AB=AC,可得∠ABC=∠ACB,分别用∠BAC、∠BCD表示出∠DAC、∠DCA,判断出∠BAC与∠BCD之间的关系即可.
解答 解:∵CD⊥AD,
∴∠CDA=90°,
∴∠DAC+∠DCA=180°-90°=90°;
∵AB=AC,
∴∠ABC=∠ACB,
∴$∠ACB=\frac{180°-∠BAC}{2}=90°-\frac{1}{2}∠BAC$;
又∵∠DAC=180°-∠BAC,
∴(180°-∠BAC)+[∠BCD-(90°-$\frac{1}{2}$∠BAC)]=90°,
∴90°-$\frac{1}{2}$∠BAC+∠BCD=90°,
∴$\frac{1}{2}$∠BAC=∠BCD,
∴∠BAC=2∠BCD.
点评 (1)此题主要考查了等腰三角形的性质和应用,考查了分类讨论思想的应用,要熟练掌握,解答此题的关键是要明确等腰三角形的性质:①等腰三角形的两腰相等;②等腰三角形的两个底角相等.③等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.
(2)此题还考查了三角形的外角的性质和应用,以及三角形的内角和定理的应用,要熟练掌握,解答此题的关键是要明确:三角形的内角和是180°.

练习册系列答案
相关题目
5.若一次函数y=2mx+(m2-2m)的图象经过坐标原点,则( )
| A. | m=0或m=2 | B. | m=0 | C. | m=2 | D. | 无法确定 |
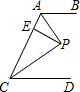 如图,AB∥CD,AP、CP分别是∠BAC和∠ACD的平分线,PE⊥AC于E,且PE=5cm,则AB与CD之间的距离是10cm.
如图,AB∥CD,AP、CP分别是∠BAC和∠ACD的平分线,PE⊥AC于E,且PE=5cm,则AB与CD之间的距离是10cm. 如图,?ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,连接AE,∠E=36°,则∠ADC的度数是54°.
如图,?ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,连接AE,∠E=36°,则∠ADC的度数是54°.