题目内容
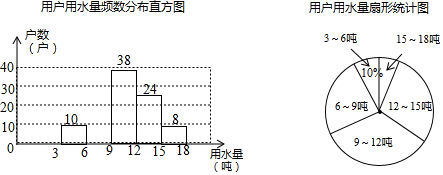
17.每年的3月22日为联合国确定的“世界水日”,某社区为了宣传节约用水,从本社区1000户家庭中随机抽取部分家庭,调查他们每月的用水量,并将调查的结果绘制成如下两幅尚不完整的统计图(每组数据包括右端点但不包括左端点),请你根据统计图解答下列问题:(1)此次抽样调查的样本容量是100;
(2)补全频数分布直方图,求扇形图中“6吨--9吨”部分的圆心角的度数;
(3)如果自来水公司将基本月用水量定为每户每月12吨,不超过基本月用水量的部分享受基本价格,超出基本月用水量的部分实行加价收费,那么该社会用户中约有多少户家庭能够全部享受基本价格?
分析 (1)由3~6吨的户数及其百分比可得样本容量;
(2)总户数减去其他分组的户数之和求得6~9吨的户数,即可补全直方图,用6~9吨的户数所占比例乘以360度可得圆心角度数;
(3)总户数乘以样本中3~12吨的户数所占比例即可得.
解答 解:(1)此次抽样调查的样本容量是10÷10%=100,
故答案为:100;
(2)6~9吨的户数为100-(10+38+24+8)=20(户),
补全频数分布直方图如下:
扇形图中“6吨--9吨”部分的圆心角的度数为360°×$\frac{20}{100}$=72°;
(3)1000×$\frac{10+20+38}{100}$=680,
答:该社区约有680户家庭的用水全部享受基本价格.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
相关题目
8.在实数3,-3,-$\sqrt{3}$,$\sqrt{3}$中最小的数是( )
| A. | 3 | B. | -3 | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
5.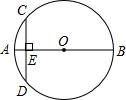 如图,AB是⊙O的直径,弦CD⊥AB于点E.若AB=8,AE=1,则弦CD的长是( )
如图,AB是⊙O的直径,弦CD⊥AB于点E.若AB=8,AE=1,则弦CD的长是( )
 如图,AB是⊙O的直径,弦CD⊥AB于点E.若AB=8,AE=1,则弦CD的长是( )
如图,AB是⊙O的直径,弦CD⊥AB于点E.若AB=8,AE=1,则弦CD的长是( )| A. | $\sqrt{7}$ | B. | 2$\sqrt{7}$ | C. | 6 | D. | 8 |
12.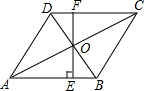 如图,在菱形ABCD中,对角线C,BD相交于点O,BD=6,AC=8,直线OE⊥AB交CD点F,则AE的长( )
如图,在菱形ABCD中,对角线C,BD相交于点O,BD=6,AC=8,直线OE⊥AB交CD点F,则AE的长( )
 如图,在菱形ABCD中,对角线C,BD相交于点O,BD=6,AC=8,直线OE⊥AB交CD点F,则AE的长( )
如图,在菱形ABCD中,对角线C,BD相交于点O,BD=6,AC=8,直线OE⊥AB交CD点F,则AE的长( )| A. | 4 | B. | 4.8 | C. | 2.4 | D. | 3.2 |
2.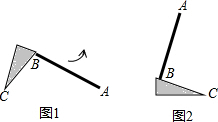 如图1,教室里有一只倒地的装垃圾的灰斗,BC与地面的夹角为50°,∠C=25°,小贤同学将它绕点C旋转一定角度,扶起平放在地面上(如图2),则灰斗柄AB绕点C转动的角度为( )
如图1,教室里有一只倒地的装垃圾的灰斗,BC与地面的夹角为50°,∠C=25°,小贤同学将它绕点C旋转一定角度,扶起平放在地面上(如图2),则灰斗柄AB绕点C转动的角度为( )
 如图1,教室里有一只倒地的装垃圾的灰斗,BC与地面的夹角为50°,∠C=25°,小贤同学将它绕点C旋转一定角度,扶起平放在地面上(如图2),则灰斗柄AB绕点C转动的角度为( )
如图1,教室里有一只倒地的装垃圾的灰斗,BC与地面的夹角为50°,∠C=25°,小贤同学将它绕点C旋转一定角度,扶起平放在地面上(如图2),则灰斗柄AB绕点C转动的角度为( )| A. | 75° | B. | 25° | C. | 115° | D. | 105° |
9.直线y=kx-1经过点A(-2,1),则不等式kx-1≥0的解集是( )
| A. | x≤-1 | B. | x≤0 | C. | x≥-1 | D. | x≥1 |
6.已知一列数:1,-2,3,-4,5,-6,7,…将这列数排成下列形式:
按照上述规律排下去,那么第100行从左边数第5个数是( )

按照上述规律排下去,那么第100行从左边数第5个数是( )
| A. | -4955 | B. | 4955 | C. | -4950 | D. | 4950 |
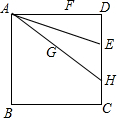 如图,正方形ABCD的边长为6,E,F分别是边CD和AD上的点,且DF=DE=2,连结AE,作点F关于AE的对称点G,连结AG并延长交CD于点H,过点G的直线l分别交线段AF,BC于点M,N,且MN=AH.则AH和MF的长分别是$\frac{15}{2}$和$\frac{13}{5}$.
如图,正方形ABCD的边长为6,E,F分别是边CD和AD上的点,且DF=DE=2,连结AE,作点F关于AE的对称点G,连结AG并延长交CD于点H,过点G的直线l分别交线段AF,BC于点M,N,且MN=AH.则AH和MF的长分别是$\frac{15}{2}$和$\frac{13}{5}$.