题目内容
8.在实数3,-3,-$\sqrt{3}$,$\sqrt{3}$中最小的数是( )| A. | 3 | B. | -3 | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
分析 正实数都大于0,负实数都小于0,正实数大于一切负实数,两个负实数绝对值大的反而小,据此判断即可.
解答 解:根据实数比较大小的方法,可得:-3<-$\sqrt{3}$<$\sqrt{3}$<3,
∴在实数3,-3,-$\sqrt{3}$,$\sqrt{3}$中最小的数是-3,
故选:B.
点评 此题主要考查了实数大小比较的方法,要熟练掌握,解答此题的关键是要明确:正实数>0>负实数,两个负实数绝对值大的反而小.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
19.计算$\frac{2}{3}$×(-$\frac{9}{4}$)的结果等于( )
| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | -$\frac{2}{3}$ | D. | $\frac{2}{3}$ |
16.在⊙O中,弦AB所对的圆心角的度数为50°,则它所对的圆周角的度数为( )
| A. | 25° | B. | 50° | C. | 25°或155° | D. | 50°或130° |
3.据统计,“五一”小长假期间,大连市共接待海内外游客825400余人次,数825100用科学记数法表示为( )
| A. | 8251×102 | B. | 825.1×103 | C. | 82.51×104 | D. | 8.251×105 |
13.一元二次方程(k-2)x2+kx+2=0(k≠2)的根的情况是( )
| A. | 该方程有两个不相等的实数根 | B. | 该方程有两个相等的实数根 | ||
| C. | 该方程有实数根 | D. | 该方程没有实数根 |
18.2017的倒数是( )
| A. | -2017 | B. | 2017 | C. | -$\frac{1}{2017}$ | D. | $\frac{1}{2017}$ |
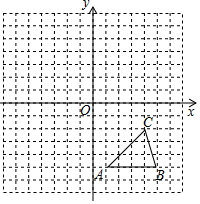 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-2).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-2).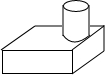 由一个圆柱与一个长方体组成的几何体如图所示,这个几何体的主视图是( )
由一个圆柱与一个长方体组成的几何体如图所示,这个几何体的主视图是( )