Question

1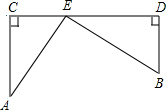．如图所示，在铁路线CD同侧有两个村庄A，B，它们到铁路线的距离分别是15km和10km，作AC⊥CD，BD⊥CD，垂足分别为C，D，且CD=25，现在要在铁路旁建一个农副产品收购站E，使A，B两村庄到收购站的距离相等，用你学过的知识，通过计算，确定点E的位置．

Answer 1

分析 关键描述语：产品收购站E，使得A、B两村到E站的距离相等，在Rt△DBE和Rt△CAE中，设出CE的长，可将AE和BE的长表示出来，列出等式进行求解即可．

解答 解：设CE=xkm，则DE=（25-x）km，
∵AC⊥CD，BD⊥CD，
∴△ACE和△BDE都是直角三角形，
在Rt△ACE中，AE²=15²+x²，
在Rt△BDE中，BE²=10²+（25-x）²，
∵AE=BE，
∴15²+x²=10²+（25-x）²，
解得：x=10，
∴E点在距离C点10km处．

点评 本题主要考查了勾股定理的应用，运用勾股定理将两个直角三角形的斜边表示出来，两边相等求解即可．