题目内容
11.平面上不重合的两点确定一条直线,不同三点最多可确定3条直线,若平面上不同的n个点最多可确定28条直线,则n的值是( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
分析 先确定两点确定一条直线;不同三点最多可确定3条直线;不同4点最多可确定(1+2+3)条直线,不同5点最多可确定(1+2+3+4)条直线,于是可根据此规律得到平面上不同的8个点最多可确定(1+2+3+4+5+6+7)=28条直线.
解答 解:两点确定一条直线;不同三点最多可确定3条直线;不同4点最多可确定(1+2+3)条直线,不同5点最多可确定(1+2+3+4)条直线,
因为1+2+3+4+5+6+7=28,
所以平面上不同的8个点最多可确定28条直线.
故选C.
点评 本题考查了直线、射线、线段:直线用一个小写字母表示,如:直线l,或用两个大写字母(直线上的)表示,如直线AB;射线是直线的一部分,用一个小写字母表示,如:射线l;用两个大写字母表示,端点在前,如:射线OA.注意:用两个字母表示时,端点的字母放在前边;线段是直线的一部分,用一个小写字母表示,如线段a;用两个表示端点的字母表示,如:线段AB(或线段BA).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.下列方程中解为x=2的是( )
| A. | 3x+(10-x)=20 | B. | 4(x+0.5)+x=7 | C. | x=-$\frac{1}{2}$x+3 | D. | $\frac{1}{7}$(x+14)=$\frac{1}{4}$(x+20) |
16.如果a的倒数是-1,那么a2等于( )
| A. | 1 | B. | -1 | C. | 3 | D. | -3 |
20.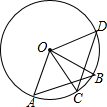 如图,在⊙O中,已知$\widehat{AB}$=$\widehat{CD}$,则AC与BD的关系是( )
如图,在⊙O中,已知$\widehat{AB}$=$\widehat{CD}$,则AC与BD的关系是( )
 如图,在⊙O中,已知$\widehat{AB}$=$\widehat{CD}$,则AC与BD的关系是( )
如图,在⊙O中,已知$\widehat{AB}$=$\widehat{CD}$,则AC与BD的关系是( )| A. | AC=BD | B. | AC<BD | C. | AC>BD | D. | 不确定 |
 如图,小明用长为3m的竹竿CD做测量共计,测量学校旗杆AB的高度,移动竹竿,使O、C、A在同一直线上,此时OD=6m,DB=12m,则旗杆AB的高为9m.
如图,小明用长为3m的竹竿CD做测量共计,测量学校旗杆AB的高度,移动竹竿,使O、C、A在同一直线上,此时OD=6m,DB=12m,则旗杆AB的高为9m.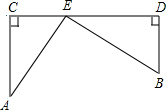 如图所示,在铁路线CD同侧有两个村庄A,B,它们到铁路线的距离分别是15km和10km,作AC⊥CD,BD⊥CD,垂足分别为C,D,且CD=25,现在要在铁路旁建一个农副产品收购站E,使A,B两村庄到收购站的距离相等,用你学过的知识,通过计算,确定点E的位置.
如图所示,在铁路线CD同侧有两个村庄A,B,它们到铁路线的距离分别是15km和10km,作AC⊥CD,BD⊥CD,垂足分别为C,D,且CD=25,现在要在铁路旁建一个农副产品收购站E,使A,B两村庄到收购站的距离相等,用你学过的知识,通过计算,确定点E的位置.