题目内容
10. 如图所示,将抛物线y=-$\frac{1}{2}$x2平移得到抛物线m,抛物线m经过点A(6,0)和原点O,它的顶点为P,它的对称轴与抛物线y=-$\frac{1}{2}$x2交于点Q,则图中阴影部分的面积为13.5.
如图所示,将抛物线y=-$\frac{1}{2}$x2平移得到抛物线m,抛物线m经过点A(6,0)和原点O,它的顶点为P,它的对称轴与抛物线y=-$\frac{1}{2}$x2交于点Q,则图中阴影部分的面积为13.5.
分析 连结OQ、OP,如图,先利用交点时写出平移后的抛物线m的解析式,再用配方得到顶点式y=-$\frac{1}{2}$(x-3)2+$\frac{9}{2}$,则P点坐标为(3,$\frac{9}{2}$),抛物线m的对称轴为直线x=3,于是可计算出Q点的坐标为(3,-$\frac{9}{2}$),所以点Q与P点关于x轴对称,于是得到图中阴影部分的面积,然后根据三角形面积公式计算.
解答  解:连结OQ、OP,如图,
解:连结OQ、OP,如图,
∵平移后的抛物线解析式为y=-$\frac{1}{2}$(x-6)•x=-$\frac{1}{2}$(x-3)2+$\frac{9}{2}$,
∴P点坐标为(3,$\frac{9}{2}$),抛物线m的对称轴为直线x=3,
当x=3时,y=-$\frac{1}{2}$x2=-$\frac{9}{2}$,则Q点的坐标为(3,-$\frac{9}{2}$),
由于抛物线y=-$\frac{1}{2}$x2向右平移3个单位,再向上平移$\frac{9}{2}$个单位得到抛物线y=-$\frac{1}{2}$(x-3)2+$\frac{9}{2}$,
所以图中阴影部分的面积=S△OPQ=$\frac{1}{2}$×3×($\frac{9}{2}$+$\frac{9}{2}$)=13.5.
故答案为:13.5.
点评 本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.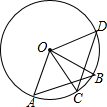 如图,在⊙O中,已知$\widehat{AB}$=$\widehat{CD}$,则AC与BD的关系是( )
如图,在⊙O中,已知$\widehat{AB}$=$\widehat{CD}$,则AC与BD的关系是( )
 如图,在⊙O中,已知$\widehat{AB}$=$\widehat{CD}$,则AC与BD的关系是( )
如图,在⊙O中,已知$\widehat{AB}$=$\widehat{CD}$,则AC与BD的关系是( )| A. | AC=BD | B. | AC<BD | C. | AC>BD | D. | 不确定 |
18.关于x的一元一次不等式x-b<0恰有两个正整数解,则b的值可能是( )
| A. | 1 | B. | 2.5 | C. | 2 | D. | 3.5 |
15. 如图所示为农村一古老的捣碎器,已知支撑柱AB的高为0.3米,踏板DE长为1米,支撑点A到踏脚D的距离为0.6米,原来捣头点E着地,现在踏脚D着地,则捣头点E上升了( )
如图所示为农村一古老的捣碎器,已知支撑柱AB的高为0.3米,踏板DE长为1米,支撑点A到踏脚D的距离为0.6米,原来捣头点E着地,现在踏脚D着地,则捣头点E上升了( )
 如图所示为农村一古老的捣碎器,已知支撑柱AB的高为0.3米,踏板DE长为1米,支撑点A到踏脚D的距离为0.6米,原来捣头点E着地,现在踏脚D着地,则捣头点E上升了( )
如图所示为农村一古老的捣碎器,已知支撑柱AB的高为0.3米,踏板DE长为1米,支撑点A到踏脚D的距离为0.6米,原来捣头点E着地,现在踏脚D着地,则捣头点E上升了( )| A. | 0.5米 | B. | 0.6米 | C. | 0.3米 | D. | 0.9米 |
19.下列长度的三条线段,能组成三角形的是( )
| A. | 3,6,9 | B. | 5,6,11 | C. | 5,6,10 | D. | 1,4,7 |
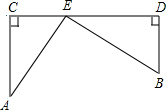 如图所示,在铁路线CD同侧有两个村庄A,B,它们到铁路线的距离分别是15km和10km,作AC⊥CD,BD⊥CD,垂足分别为C,D,且CD=25,现在要在铁路旁建一个农副产品收购站E,使A,B两村庄到收购站的距离相等,用你学过的知识,通过计算,确定点E的位置.
如图所示,在铁路线CD同侧有两个村庄A,B,它们到铁路线的距离分别是15km和10km,作AC⊥CD,BD⊥CD,垂足分别为C,D,且CD=25,现在要在铁路旁建一个农副产品收购站E,使A,B两村庄到收购站的距离相等,用你学过的知识,通过计算,确定点E的位置. 如图,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC、AB分别交于点D、E,且∠CBD=∠A.
如图,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC、AB分别交于点D、E,且∠CBD=∠A.